P.A. resolução de problema

por **aliceit** » Ter Abr 26, 2011 22:52

Uma indústria de produtos natalinos encerrou o ano de 2006, com um estoque de 250 peças. Em janeiro de 2007, a indústria concedeu férias coletivas a seus funcionários e a partir de fevereiro recomeçou sua produção. Com base no texto, considerando que essa indústria, em fevereiro, produziu 550 produtos, que a cada mês essa produção cresceu em progressão aritmética e que em novembro de 2007 o estoque passou a ter 26000 itens, é correto afirmar que o número de peças produzidas em agosto foi de..?

Eu tentei a soma dos termos da P.A., juntando primeiro o 250 com o 550 (produção de fevereiro):
S10 = a1 + a10 * 10/5
26.000 = 800 + a10 * 10/5
a10 = 4400

depois eu coloquei na forma do termo geral:
a10 = a1 + 9R
4400 = 800 + 9R
R = 400

então, apliquei no termo geral para saber o mês de agosto:
a7 = a1 + 6R
a7 = 800 + 6*400

a resposta é 3250!, mas só acho 3200
por favor, me ajudem!!

por **MarceloFantini** » Qua Abr 27, 2011 00:36

Você errou aqui: primeiro, novembro é a_9

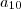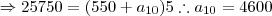
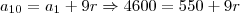
e não $a_{10}$ ; segundo, quando você trabalha com peças produzidas, você não conta o estoque do ano 2006 - você quer apenas as peças produzidas a cada mês, e as peças de 2006 não foram produzidas em 2007 (óbvio, sim). Refaça suas contas e chegará ao resultado certo.

por **aliceit** » Qua Abr 27, 2011 10:31

olá!

obrigada por dispensar seu tempo para me ajudar.
eu tentei fazer o que você disse: novembro como a9, e desprezei o estoque de 2006.
no entanto a conta ficou muito esquisita e não cheguei ao resultado.

vou continuar tentando,

valeu!

por **MarceloFantini** » Qua Abr 27, 2011 19:46

Cacete (desculpe), cometi um erro e ainda por cima tive um tremendo trabalho refazendo meus passos pra descobrir como cheguei na resposta. Aqui vai:

Primeiro, você estava certo. É $a_{10}$ mesmo, perdão pelo erro!

Segundo, a resolução segue assim:

A soma de todos as produções JUNTAMENTE com o estoque antigo deve somar 26000, logo:

$S_{10} = \frac{(a_1 + a_{10})10}{2} + 250 \Rightarrow 26000 = (550 + a_{10})5 + 250$

$\Rightarrow 25750 = (550 + a_{10})5 \therefore a_{10} = 4600$

Usando a definição de termo geral de P.A.:

$a_{10} = a_1 + 9r \Rightarrow 4600 = 550 + 9r$

$\therefore r = 450$

Calculando o número de peças em agosto:

$a_7 = a_1 +6r \Rightarrow a_7 = 550 + 6 \cdot 450$

$\therefore a_7 = 3250$

por **aliceit** » Qua Abr 27, 2011 23:22

Fantini,
super agradeço a sua colaboração!
hoje a noite consegui resolver a questão, e quando loguei aqui para te mostrar vi a surpresa!
digamos que a sua resolução ficou mais organizada que a minha, hauahuahua.

mais uma vez obrigada,
muita paz e muito sucesso na sua vida!

por **MarceloFantini** » Qua Abr 27, 2011 23:30

É uma resolução bem explicada e resolvida, como os alunos deveriam ser ensinados no ensino médio, e não álgebras sem explicações. Fico feliz que apesar do meu erro você tenha conseguido por conta própria! Muita paz e sucesso para você também.