 por willwgo » Qua Abr 27, 2011 17:58
por willwgo » Qua Abr 27, 2011 17:58
7- calcule o valor de A, sabendo que :
a) p(x)=

é divisivel por h(x)= x-1;
b)p(x)=
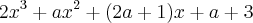
é divisivel por x+4.
8-(puc-sp) calcule os valore de A e B para que os polinômios p(x)=

seja divisivel por g(x)=
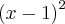
nau consgui resolver de jeito nenhum esse exercício, usei a fórmula de briot-ruffini!
me ajudem ai, se conseguirem chegar a resposta me digam como fizeram e qual fórmula usaram!
obrigado.
-
willwgo
- Usuário Dedicado

-
- Mensagens: 33
- Registrado em: Qui Fev 17, 2011 15:59
- Formação Escolar: ENSINO MÉDIO
- Andamento: formado
 por Fabricio dalla » Qua Abr 27, 2011 19:22
por Fabricio dalla » Qua Abr 27, 2011 19:22
orientaçao para o exercicio 7
quando um polinomio e divisivel por outro podemos afirmar que a raiz do polinomio divisor tbm é raiz do outro polinomio
na letra (a 1 e raiz polinomio
(b: -4 e raiz do outro polinomio
8)a ideia é a mesma da 7. 1 vai ter q ser raiz de p(x) para que seja divisivel
-
Fabricio dalla
- Colaborador Voluntário

-
- Mensagens: 111
- Registrado em: Sáb Fev 26, 2011 17:50
- Formação Escolar: ENSINO MÉDIO
- Andamento: formado
 por willwgo » Qui Abr 28, 2011 17:22
por willwgo » Qui Abr 28, 2011 17:22
obrigado
-
willwgo
- Usuário Dedicado

-
- Mensagens: 33
- Registrado em: Qui Fev 17, 2011 15:59
- Formação Escolar: ENSINO MÉDIO
- Andamento: formado
Voltar para Polinômios
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- [Calcule o valor de Seno de 18º] Expressar o valor numérico
por VictorFPS » Sáb Fev 14, 2015 20:01
- 1 Respostas
- 3864 Exibições
- Última mensagem por adauto martins

Qui Fev 19, 2015 15:41
Trigonometria
-
- Calcule o valor de x
por thadeu » Ter Jun 29, 2010 20:26
- 2 Respostas
- 7569 Exibições
- Última mensagem por thadeu

Ter Jun 29, 2010 21:29
Piadas
-
- Calcule o valor de x
por andersontricordiano » Seg Fev 24, 2014 16:09
- 1 Respostas
- 1739 Exibições
- Última mensagem por Man Utd

Seg Fev 24, 2014 17:04
Números Complexos
-
- calcule o valor de x
 por leticiapires52 » Sex Mai 09, 2014 15:09
por leticiapires52 » Sex Mai 09, 2014 15:09
- 6 Respostas
- 4058 Exibições
- Última mensagem por leticiapires52

Sex Mai 09, 2014 19:04
Logaritmos
-
- (UF-MG) Calcule o valor de A3/A2 do triângulo abaixo
 por andersontricordiano » Qua Mar 09, 2011 13:04
por andersontricordiano » Qua Mar 09, 2011 13:04
- 1 Respostas
- 2385 Exibições
- Última mensagem por andersontricordiano

Qua Mar 16, 2011 12:19
Geometria
Usuários navegando neste fórum: Nenhum usuário registrado e 0 visitantes
Assunto:
cálculo de limites
Autor:
Hansegon - Seg Ago 25, 2008 11:29
Bom dia.
Preciso de ajuda na solução deste problema, pois só chego ao resultado de 0 sobre 0.
Obrigado
\lim_{x\rightarrow-1} x³ +1/x²-1[/tex]
Assunto:
cálculo de limites
Autor:
Molina - Seg Ago 25, 2008 13:25

Realmente se você jogar o -1 na equação dá 0 sobre 0.
Indeterminações deste tipo você pode resolver por L'Hôpital
que utiliza derivada.
Outro modo é transformar o numerador e/ou denominador
para que não continue dando indeterminado.
Dica: dividir o numerador e o denominador por algum valor é uma forma que normalmente dá certo.

Caso ainda não tenha dado uma

, avisa que eu resolvo.
Bom estudo!
Assunto:
cálculo de limites
Autor:
Guill - Dom Abr 08, 2012 16:03



Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
 é divisivel por h(x)= x-1;
é divisivel por h(x)= x-1;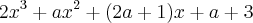 é divisivel por x+4.
é divisivel por x+4. seja divisivel por g(x)=
seja divisivel por g(x)=





 , avisa que eu resolvo.
, avisa que eu resolvo.

