 por rafaelrosa » Seg Abr 25, 2011 11:03
por rafaelrosa » Seg Abr 25, 2011 11:03
Estou com alguns problemas com calculo de matrizes, estou com o seguinte exercício:
Sabendo que a=2 1 , b=-1 2 e c=4-1 calcule a matriz x.
3-1 1 0 2 1
No caso a matriz x seria o resultado da multiplicação das 3 matrizes? sendo x= -8-2 ?
6 0
-
rafaelrosa
- Novo Usuário

-
- Mensagens: 5
- Registrado em: Seg Abr 25, 2011 10:25
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Civíl
- Andamento: cursando
 por LuizAquino » Seg Abr 25, 2011 13:55
por LuizAquino » Seg Abr 25, 2011 13:55
Por favor, digite as matrizes usando a notação adequada.
Por exemplo, para digitar a matriz

use o comando tex:
- Código: Selecionar todos
[tex]A=\begin{bmatrix} a & b \\ c & d \end{bmatrix}[/tex]
Você também pode usar o
Editor de Fórmulas aqui do fórum.
Além disso, eu gostaria de recomendar que você assista as vídeo-aulas do Nerckie sobre matrizes. O título do vídeo é "Matemática - Aula 19 - Matrizes - Conceitos Iniciais" e ele está dividido em 5 partes. O endereço do canal é:
http://www.youtube.com/nerckie
-

LuizAquino
- Colaborador Moderador - Professor

-
- Mensagens: 2654
- Registrado em: Sex Jan 21, 2011 09:11
- Localização: Teófilo Otoni - MG
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Mestrado - Modelagem Computacional
- Andamento: formado
-
 por rafaelrosa » Ter Abr 26, 2011 12:12
por rafaelrosa » Ter Abr 26, 2011 12:12
Editando...
Eu tinha copiado errado a questão, o correto é:
Determine a matriz x:
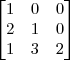
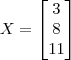
O que eu tentei fazer é: já que a primeira matriz é 3x
3 e a segunda é
3x1 a determinando ficaria 3x1, com isto:
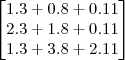
=

Editado pela última vez por
rafaelrosa em Ter Abr 26, 2011 12:20, em um total de 1 vez.
-
rafaelrosa
- Novo Usuário

-
- Mensagens: 5
- Registrado em: Seg Abr 25, 2011 10:25
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Civíl
- Andamento: cursando
 por LuizAquino » Ter Abr 26, 2011 12:19
por LuizAquino » Ter Abr 26, 2011 12:19
Para resolver a equação matricial

você precisa determinar a matriz inversa de
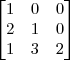
.
Em seguida, basta calcular o produto:
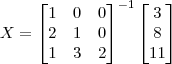
Outra opção seria escrever
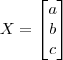
e a partir daí resolver o sistema:
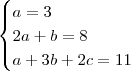 Observação
ObservaçãoNo canal do
Nerckie também há vídeo-aulas sobre o cálculo de matrizes inversas.
Editado pela última vez por
LuizAquino em Ter Abr 26, 2011 12:37, em um total de 2 vezes.
-

LuizAquino
- Colaborador Moderador - Professor

-
- Mensagens: 2654
- Registrado em: Sex Jan 21, 2011 09:11
- Localização: Teófilo Otoni - MG
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Mestrado - Modelagem Computacional
- Andamento: formado
-
 por rafaelrosa » Ter Abr 26, 2011 12:26
por rafaelrosa » Ter Abr 26, 2011 12:26
LuizAquino escreveu:Para resolver a equação matricial

você precisa determinar a matriz inversa de
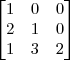
.
Em seguida, basta calcular o produto:
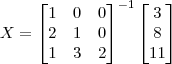 Observação
ObservaçãoNo canal do
Nerckie também há vídeo-aulas sobre o cálculo de matrizes inversas.
Então ficaria:

x
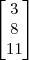
=

?
Estou no trabalho, a noite vejo a aula no youtube...
-
rafaelrosa
- Novo Usuário

-
- Mensagens: 5
- Registrado em: Seg Abr 25, 2011 10:25
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Civíl
- Andamento: cursando
 por LuizAquino » Qua Abr 27, 2011 10:24
por LuizAquino » Qua Abr 27, 2011 10:24
Temos que
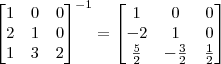
.
Sendo assim, você precisa resolver:
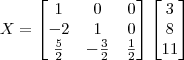
-

LuizAquino
- Colaborador Moderador - Professor

-
- Mensagens: 2654
- Registrado em: Sex Jan 21, 2011 09:11
- Localização: Teófilo Otoni - MG
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Mestrado - Modelagem Computacional
- Andamento: formado
-
Voltar para Matrizes e Determinantes
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- calcular matriz
por rodrigonapoleao » Qua Jan 02, 2013 20:19
- 1 Respostas
- 2526 Exibições
- Última mensagem por e8group

Qua Jan 02, 2013 20:51
Matrizes e Determinantes
-
- [É possível Calcular Matriz Forçada 2x2?]
por Markus » Dom Jan 29, 2012 19:50
- 2 Respostas
- 2367 Exibições
- Última mensagem por Markus

Ter Jan 31, 2012 13:41
Matrizes e Determinantes
-
- Calcular determinante de matriz com 3 incógnitas
por Sherminator » Sáb Nov 24, 2012 09:10
- 4 Respostas
- 8776 Exibições
- Última mensagem por Sherminator

Sáb Nov 24, 2012 12:38
Matrizes e Determinantes
-
- Como calcular o determinante inversa da Matriz ?
por gustavosec » Sáb Mar 26, 2016 16:55
- 1 Respostas
- 16158 Exibições
- Última mensagem por vitor_jo

Sáb Jul 16, 2016 03:17
Matrizes e Determinantes
-
- [MATRIZ] Como acho o determinante dessa matriz
por LAZAROTTI » Qui Mai 03, 2012 00:38
- 4 Respostas
- 7160 Exibições
- Última mensagem por Russman

Qui Mai 03, 2012 01:56
Matrizes e Determinantes
Usuários navegando neste fórum: Nenhum usuário registrado e 0 visitantes
Assunto:
simplifiquei e achei...está certo?????????????
Autor:
zig - Sex Set 23, 2011 13:57
![{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]} {(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]}](/latexrender/pictures/19807748a214d3361336324f3e43ea9a.png)
![{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}} {(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}}](/latexrender/pictures/3d7908e5b4e397bf635b6546063d9130.png)
Assunto:
simplifiquei e achei...está certo?????????????
Autor:
Vennom - Sex Set 23, 2011 21:41
zig escreveu:![{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]} {(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]}](/latexrender/pictures/19807748a214d3361336324f3e43ea9a.png)
![{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}} {(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}}](/latexrender/pictures/3d7908e5b4e397bf635b6546063d9130.png)
Rpz, o negócio é o seguinte:
Quando você tem uma potência negativa, tu deve inverter a base dela. Por exemplo:

Então pense o seguinte: a fração geratriz de 0,05 é

, ou seja, 1 dividido por 20 é igual a 0.05 . Sendo assim, a função final é igual a vinte elevado à meio.
Veja:
![{0,05}^{-\frac{1}{2}} = {\frac{1}{20}}^{-\frac{1}{2}} = {\frac{20}{1}}^{\frac{1}{2}} = \sqrt[2]{20} {0,05}^{-\frac{1}{2}} = {\frac{1}{20}}^{-\frac{1}{2}} = {\frac{20}{1}}^{\frac{1}{2}} = \sqrt[2]{20}](/latexrender/pictures/c0100c6f4d8bdbb7d54165e6be7aff04.png)
A raiz quadrada de vinte, você acha fácil, né?
Espero ter ajudado.
Assunto:
simplifiquei e achei...está certo?????????????
Autor:
fraol - Dom Dez 11, 2011 20:23
Nós podemos simplificar, um pouco,

da seguinte forma:

.
É isso.
Assunto:
simplifiquei e achei...está certo?????????????
Autor:
fraol - Dom Dez 11, 2011 20:24
Nós podemos simplificar, um pouco,

da seguinte forma:

.
É isso.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.


 use o comando tex:
use o comando tex:
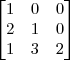
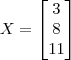
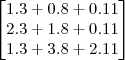 =
= 
 você precisa determinar a matriz inversa de
você precisa determinar a matriz inversa de 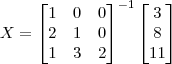
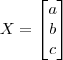 e a partir daí resolver o sistema:
e a partir daí resolver o sistema: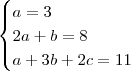
 x
x 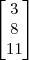 =
=  ?
?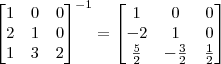 .
.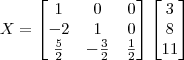
![{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]} {(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]}](/latexrender/pictures/19807748a214d3361336324f3e43ea9a.png)
![{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}} {(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}}](/latexrender/pictures/3d7908e5b4e397bf635b6546063d9130.png)

 , ou seja, 1 dividido por 20 é igual a 0.05 . Sendo assim, a função final é igual a vinte elevado à meio.
, ou seja, 1 dividido por 20 é igual a 0.05 . Sendo assim, a função final é igual a vinte elevado à meio. ![{0,05}^{-\frac{1}{2}} = {\frac{1}{20}}^{-\frac{1}{2}} = {\frac{20}{1}}^{\frac{1}{2}} = \sqrt[2]{20} {0,05}^{-\frac{1}{2}} = {\frac{1}{20}}^{-\frac{1}{2}} = {\frac{20}{1}}^{\frac{1}{2}} = \sqrt[2]{20}](/latexrender/pictures/c0100c6f4d8bdbb7d54165e6be7aff04.png)
 da seguinte forma:
da seguinte forma: .
. da seguinte forma:
da seguinte forma: .
.