Olá, sou um analista de sistemas e me deparei com um problema aqui que na teoria seria simples, mais ta me dando a maior dor de cabeça.
O problema é o seguinte, preciso descobrir se 3 pontos no espaço são colineares, pela referência matemátcia que tenho, deveria jogar esses pontos em uma matriz e calcular o seu determinante, caso o determinante seja zero isso significa que os pontos são colineares.
Porém estou tendo dificuldades com este problema pois, suponhamos que existem 3 pontos onde o eixo z de todos é igual a zero, neste caso a determinante será sempre zero e não necessáriamente os pontos são colineares.
Será que poderiam me ajudar nessa questão?
Desde já agradeço
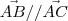. Ou seja, se existe um escalar 
.
por ![{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]}](/latexrender/pictures/19807748a214d3361336324f3e43ea9a.png "{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]}")
![{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}}](/latexrender/pictures/3d7908e5b4e397bf635b6546063d9130.png "{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}}")
, ou seja, 1 dividido por 20 é igual a 0.05 . Sendo assim, a função final é igual a vinte elevado à meio. ![{0,05}^{-\frac{1}{2}} = {\frac{1}{20}}^{-\frac{1}{2}} = {\frac{20}{1}}^{\frac{1}{2}} = \sqrt[2]{20}](/latexrender/pictures/c0100c6f4d8bdbb7d54165e6be7aff04.png "{0,05}^{-\frac{1}{2}} = {\frac{1}{20}}^{-\frac{1}{2}} = {\frac{20}{1}}^{\frac{1}{2}} = \sqrt[2]{20}")
da seguinte forma:
.
da seguinte forma:
.