 por marioitalo » Qua Out 15, 2008 20:26
por marioitalo » Qua Out 15, 2008 20:26
Olá a todos,
Estive lendo a resolução de um problema que consistia em provar que

, o que é equivalente a

Pois bem, acontece que o primeiro passo para quem elaborou o gabarito foi transformar
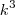
em

Não consigo entender de onde saiu essa expressão. Consegui enxergar apenas que

foi fatorado de

, que

foi fatorado de

e

de

Alguém pode me socorrer, porque estou há um tempão tentando enxergar de onde surgiu esse desdobramento, se foi baseado em algum teorema, se foi por derivada, integral, intuição... O pior é que deve ser algo bem banal e tá me deixando maluco.
-
marioitalo
- Novo Usuário

-
- Mensagens: 3
- Registrado em: Qua Out 15, 2008 20:02
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Tecnologia em Sistemas da Computação
- Andamento: cursando
 por admin » Sex Out 17, 2008 05:33
por admin » Sex Out 17, 2008 05:33
Olá
marioitalo, boas-vindas!
Somente partindo desta expansão em particular eu ainda também não percebi qual foi a expressão considerada inicialmente e o objetivo na demonstração. Talvez a idéia fique mais clara enviando a resolução completa para apreciarmos.
Vale dizer que não há apenas uma prova ou demonstração para esta soma de cubos, há várias.
Não sei se sua dúvida é apenas esta ou se a idéia de outra demonstração ajudaria.
Por exemplo, uma possibilidade é considerar a seguinte expansão:

E antes de variarmos

de

a

, escrevemos assim:

Fazendo

variar, temos:

Repare que somando todos os membros, do lado esquerdo teremos vários cancelamentos, e do lado direito colocamos em evidência a soma dos cubos, dos quadrados e dos naturais:

Chamando de


Agora consideramos a soma dos quadrados obtida de forma análoga:

E também esta mais comum:


Expandindo a quarta potência, fazendo as outras distributivas e isolando

, obtemos:
![S = \left[ \frac{n(n+1)}{2} \right]^2 S = \left[ \frac{n(n+1)}{2} \right]^2](/latexrender/pictures/4821ca5ca58652f298baeddc25359095.png)
Até mais!
-

admin
- Colaborador Administrador - Professor

-
- Mensagens: 885
- Registrado em: Qui Jul 19, 2007 10:58
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Licenciatura em Matemática IME-USP
- Andamento: formado
 por marioitalo » Sex Out 17, 2008 15:41
por marioitalo » Sex Out 17, 2008 15:41
Muito obrigado pela resposta e pelas boas vindas, Fabio.
Segue abaixo o desenvolvimento completo da questão.
Obs.: Eu consegui chegar à expressão

fazendo a expansão de

, como se fosse

considerando

e
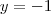
e rearrumando os termos, mas ainda assim não sei como se chegou àquela outra expressão.
Abraço.
Editado pela última vez por
marioitalo em Sex Out 17, 2008 23:41, em um total de 1 vez.
-
marioitalo
- Novo Usuário

-
- Mensagens: 3
- Registrado em: Qua Out 15, 2008 20:02
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Tecnologia em Sistemas da Computação
- Andamento: cursando
 por admin » Sex Out 17, 2008 18:03
por admin » Sex Out 17, 2008 18:03
Olá
marioitalo!
Agora a idéia criativa da demonstração ficou mais clara.
Antes, um detalhe de edição que percebi: na segunda parte, 2ª e 3ª linhas, faltou o símbolo fatorial em

.
Sobre a sua dúvida para a escolha de
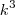
daquela forma, podemos dizer que sim, foi uma "intuição" tática.
A origem desta idéia surge ao observar onde queremos chegar, ou seja:
![S = \left[ \frac{n(n+1)}{2} \right]^2 S = \left[ \frac{n(n+1)}{2} \right]^2](/latexrender/pictures/4821ca5ca58652f298baeddc25359095.png)
Em destaque, este produto:

.
Quem criou a demonstração queria "fazer surgir" fatoriais para após as simplificações ficar com o produto

.
Note que
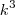
pode ser representado de outras formas conforme conveniência na prova.
Como aquela foi a escolha, estas são as condições para que a expressão se mantenha verdadeira:
De modo que os termos de grau 2 e 1 sejam anulados, ficando o de grau 3 com coeficiente 1:

Há outras demonstrações também bem interessantes e criativas. Li sobre uma geométrica que consta no livro do Simmons, cálculo com geometria analítica. Meu livro deve chegar na próxima semana, caso não tenha e queira ver posso postar depois por aqui.
Bons estudos!
-

admin
- Colaborador Administrador - Professor

-
- Mensagens: 885
- Registrado em: Qui Jul 19, 2007 10:58
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Licenciatura em Matemática IME-USP
- Andamento: formado
 por marioitalo » Dom Out 19, 2008 03:05
por marioitalo » Dom Out 19, 2008 03:05
Olá Fabio,
Desculpe a demora em responder, mas é que comecei a seguir uma série de sites sobre o assunto que me levaram até aqui:
http://en.wikipedia.org/wiki/Pochhammer_symbol, uma página da Wikipedia falando sobre o símbolo de Pochhammer, que representa o "rising sequential product" ou fatorial ascendente (não sei se a tradução é exatamente essa), que guarda grande similaridade com a tal expressão inicial que postei. Pesquisando mais um puco, cheguei a esse PDF:
http://www.escolademestres.com/qedtexte/tomo1serieamostra.pdf, um manual de seqüências e séries. Lá pela página 14 ele resolve o mesmo problema usando o tal produto fatorial, com a diferença que lá ele usa o descendente e naquela demonstração que postei acredito que tenha sido usado o ascendente.
É mais ou menos assim: Seja

um polinômio fatorial da forma

Considerando que:
Podemos exprimir um polinômio

em função dos polinômios fatoriais

sendo

e

os restos das divisões abaixo:




Achando esses restos

, já caimos direto na expressão que foi utilizada dentro do somatório na resolução postada anteriormente, qual seja:

Se não quisermos obter esses restos, basta atribuir

como foi feito naquele primeiro caso e, ao final, zerarmos os coeficientes de
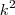
e



E aqui finalmente a bendita expressão aparece!
Bem, é isso. Se eu escrevi alguma besteira, por favor me corrijam...
Obrigado pela ajuda, Fabio.
Abraço.
-
marioitalo
- Novo Usuário

-
- Mensagens: 3
- Registrado em: Qua Out 15, 2008 20:02
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Tecnologia em Sistemas da Computação
- Andamento: cursando
 por admin » Ter Out 28, 2008 15:40
por admin » Ter Out 28, 2008 15:40
Olá
marioitalo!
Também peço desculpas pela demora em responder, mas atualmente não estou tão presente por aqui.
Eu também não conhecia aquela forma simplificada de representar os produtos.
É mais uma evidência da necessidade em cálculos deste tipo, visando facilitar a notação.
Aproveito para dar parabéns ao seu interesse em pesquisar!
Eu havia comentado sobre uma demonstração geométrica que consta no livro do Simmons, veja que interessante.
Antes, o autor destaca que a prova partindo desta expressão

é apenas uma extensão da idéia "do grande teólogo-matemático-cientista-escritor francês Blaise Pascal" que provou a fórmula para a soma dos

primeiros quadrados a partir desta expansão:

Eis a demonstração geométrica:
Começando no ponto

, assentamos segmentos sucessivos de comprimentos

etc. e finalmente um de comprimento

atingindo o ponto

.
Fazemos o mesmo sobre a reta

perpendicular a
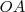
, de modo que

A área do quadrado é, portanto,
![S = \left[ \frac{n(n+1)}{2} \right]^2 \;\;\;\;\;\;\;\;\;\; (I) S = \left[ \frac{n(n+1)}{2} \right]^2 \;\;\;\;\;\;\;\;\;\; (I)](/latexrender/pictures/ef1e8ba07673690d2ed033da1ee52ff1.png)
Entretanto, o quadrado é a soma de

regiões em forma de

, indicadas na figura:

Qual é a área de

? Essa região pode ser dividida em dois retângulos, como na figura. Assim
![L_n = n \left[ \frac{n(n+1)}{2} \right] + n \left[ \frac{(n-1)n}{2} \right] L_n = n \left[ \frac{n(n+1)}{2} \right] + n \left[ \frac{(n-1)n}{2} \right]](/latexrender/pictures/dc5e67880aa252f02d42941ed68fe34a.png)
![= \frac12 n^2 \left[ (n+1)+(n-1) \right] = n^3 = \frac12 n^2 \left[ (n+1)+(n-1) \right] = n^3](/latexrender/pictures/498ab8afa9df2fb164437055465b4ad7.png)
Conseqüentemente,

e comparando
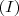
e
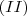
temos
![1^3 + 2^3 + \cdots + n^3 = \left[ \frac{n(n+1)}{2} \right]^2 1^3 + 2^3 + \cdots + n^3 = \left[ \frac{n(n+1)}{2} \right]^2](/latexrender/pictures/0bd14a9561c0c92449b75c5655e22aa0.png)
Bons estudos e até mais!
-

admin
- Colaborador Administrador - Professor

-
- Mensagens: 885
- Registrado em: Qui Jul 19, 2007 10:58
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Licenciatura em Matemática IME-USP
- Andamento: formado
Voltar para Polinômios
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- [Transformação Linear] Nucleo e Imagem, ache a transformaçao
por vualas » Qua Nov 07, 2012 00:37
- 2 Respostas
- 4244 Exibições
- Última mensagem por adauto martins

Qui Dez 15, 2016 11:12
Álgebra Linear
-
- [polinômio]Relações de Girard + raízes de polinômio
por matano2104 » Qui Set 05, 2013 17:02
- 1 Respostas
- 7150 Exibições
- Última mensagem por young_jedi

Qui Set 05, 2013 17:57
Polinômios
-
- Transformação
por barbara-rabello » Ter Nov 20, 2012 14:30
- 1 Respostas
- 1844 Exibições
- Última mensagem por MarceloFantini

Ter Nov 20, 2012 15:02
Álgebra Linear
-
- transformação
por zenildo » Qui Jun 05, 2014 23:53
- 1 Respostas
- 2720 Exibições
- Última mensagem por Russman

Sex Jun 06, 2014 01:53
Conversão de Unidades
-
- Transformação em produto
 por Ananda » Seg Mar 24, 2008 17:31
por Ananda » Seg Mar 24, 2008 17:31
- 3 Respostas
- 5504 Exibições
- Última mensagem por Ananda

Ter Mar 25, 2008 14:55
Trigonometria
Usuários navegando neste fórum: Nenhum usuário registrado e 0 visitantes
Assunto:
método de contagem
Autor:
sinuca147 - Seg Mai 25, 2009 09:10
Veja este exercício:
Se A = {

} e B = {

}, então o número de elementos A

B é:
Eu tentei resolver este exercício e achei a resposta "três", mas surgiram muitas dúvidas aqui durante a resolução.
Para determinar os elementos do conjunto A, eu tive de basicamente fazer um lista de vinte dividido por todos os números naturais maiores que zero e menores que vinte e um, finalmente identificando como elementos do conjunto A os números 1, 2, 4, 5, 10 e 20. Acho que procedi de maneira correta, mas fiquei pensando aqui se não existiria um método mais "sofisticado" e prático para que eu pudesse identificar ou ao menos contar o número de elementos do conjunto A, existe?
No processo de determinação dos elementos do conjunto B o que achei foi basicamente os múltiplos de cinco e seus opostos, daí me surgiram estas dúvidas:
existe oposto de zero?
existe inverso de zero?
zero é par, certo?
sendo x um número natural, -x é múltiplo de x?
sendo z um número inteiro negativo, z é múltiplo de z?
sendo z um número inteiro negativo, -z é múltiplo de z?
A resposta é 3?
Obrigado.
Assunto:
método de contagem
Autor:
Molina - Seg Mai 25, 2009 20:42
Boa noite, sinuca.
Se A = {

} você concorda que n só pode ser de 1 a 20? Já que pertence aos naturais?
Ou seja, quais são os divisores de 20? Eles são seis: 1, 2, 4, 5, 10 e 20.
Logo, o conjunto A é
A = {1, 2, 4, 5, 10, 20}
Se B = {

} você concorda que x será os múltiplos de 5 (positivos e negativos)? Já que m pertence ao conjunto Z?
Logo, o conjunto B é
B = {... , -25, -20, -15, -10, -5, 0, 5, 10, 15, 20, 25, ...
Feito isso precisamos ver os números que está em ambos os conjuntos, que são:
5, 10 e 20 (3 valores, como você achou).
Vou responder rapidamente suas dúvidas porque meu tempo está estourando. Qualquer dúvida, coloque aqui, ok?
sinuca147 escreveu:No processo de determinação dos elementos do conjunto B o que achei foi basicamente os múltiplos de cinco e seus opostos, daí me surgiram estas dúvidas:
existe oposto de zero? sim, é o próprio zero
existe inverso de zero? não, pois não há nenhum número que multiplicado por zero resulte em 1
zero é par, certo? sim, pois pode ser escrito da forma de 2n, onde n pertence aos inteiros
sendo x um número natural, -x é múltiplo de x? Sim, pois basta pegar x e multiplicar por -1 que encontramos -x
sendo z um número inteiro negativo, z é múltiplo de z? Sim, tais perguntando se todo número é multiplo de si mesmo
sendo z um número inteiro negativo, -z é múltiplo de z? Sim, pois basta pegar -z e multiplicar por -1 que encontramos x
A resposta é 3? Sim, pelo menos foi o que vimos a cima
Bom estudo,

Assunto:
método de contagem
Autor:
sinuca147 - Seg Mai 25, 2009 23:35
Obrigado, mas olha só este link
http://www.colegioweb.com.br/matematica ... ro-natural
neste link encontra-se a a frase:
Múltiplo de um número natural é qualquer número que possa ser obtido multiplicando o número natural por 0, 1, 2, 3, 4, 5, etc.
Para determinarmos os múltiplos de 15, por exemplo, devemos multiplicá-lo pela sucessão dos números naturais:
Ou seja, de acordo com este link -5 não poderia ser múltiplo de 5, assim como 5 não poderia ser múltiplo de -5, eu sempre achei que não interessava o sinal na questão dos múltiplos, assim como você me confirmou, mas e essa informação contrária deste site, tem alguma credibilidade?
Há e claro, a coisa mais bacana você esqueceu, quero saber se existe algum método de contagem diferente do manual neste caso:
Para determinar os elementos do conjunto A, eu tive de basicamente fazer um lista de vinte dividido por todos os números naturais maiores que zero e menores que vinte e um, finalmente identificando como elementos do conjunto A os números 1, 2, 4, 5, 10 e 20. Acho que procedi de maneira correta, mas fiquei pensando aqui se não existiria um método mais "sofisticado" e prático para que eu pudesse identificar ou ao menos contar o número de elementos do conjunto A, existe?
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
 , o que é equivalente a
, o que é equivalente a 
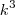 em
em
 foi fatorado de
foi fatorado de  , que
, que  foi fatorado de
foi fatorado de  e
e  de
de 



 de
de  a
a  , escrevemos assim:
, escrevemos assim:







 , obtemos:
, obtemos:![S = \left[ \frac{n(n+1)}{2} \right]^2 S = \left[ \frac{n(n+1)}{2} \right]^2](/latexrender/pictures/4821ca5ca58652f298baeddc25359095.png)

 fazendo a expansão de
fazendo a expansão de  , como se fosse
, como se fosse  considerando
considerando  e
e 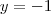 e rearrumando os termos, mas ainda assim não sei como se chegou àquela outra expressão.
e rearrumando os termos, mas ainda assim não sei como se chegou àquela outra expressão.












![=3!\sum_{k=1}^{n}\frac{(k+2)!}{(k-1)!3!}=3![C(3,3)+...+C(n+2,3)] =3!\sum_{k=1}^{n}\frac{(k+2)!}{(k-1)!3!}=3![C(3,3)+...+C(n+2,3)]](/latexrender/pictures/0f32f69c690f7d5eeba58eaefe11a409.png)
![=3![C(n+3,4)] =3![C(n+3,4)]](/latexrender/pictures/3bc0ff02fadcd0c7585a8e2ce37f28a7.png) (pelo teorema das colunas do triângulo de Pascal)
(pelo teorema das colunas do triângulo de Pascal)




![=2![C(2,2)+C(3,2)+...+C(n+1,2)]=2![C(n+2,3)] =2![C(2,2)+C(3,2)+...+C(n+1,2)]=2![C(n+2,3)]](/latexrender/pictures/5049f994e27110d41dfe241cfc50e923.png) (pelo teorema das colunas)
(pelo teorema das colunas)

 (pelo teorema das colunas)
(pelo teorema das colunas)





![=\frac{n(n+1)[3(n+2)(n+3)-12(n+2)+6n]}{12} =\frac{n(n+1)[3(n+2)(n+3)-12(n+2)+6n]}{12}](/latexrender/pictures/9bccca4cf5f59885edb45684aa6dc608.png)



 .
. .
.
 um polinômio fatorial da forma
um polinômio fatorial da forma 
 em função dos polinômios fatoriais
em função dos polinômios fatoriais  sendo
sendo  e
e  os restos das divisões abaixo:
os restos das divisões abaixo:



 , já caimos direto na expressão que foi utilizada dentro do somatório na resolução postada anteriormente, qual seja:
, já caimos direto na expressão que foi utilizada dentro do somatório na resolução postada anteriormente, qual seja:
 como foi feito naquele primeiro caso e, ao final, zerarmos os coeficientes de
como foi feito naquele primeiro caso e, ao final, zerarmos os coeficientes de 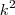 e
e 



 , assentamos segmentos sucessivos de comprimentos
, assentamos segmentos sucessivos de comprimentos  etc. e finalmente um de comprimento
etc. e finalmente um de comprimento  .
. perpendicular a
perpendicular a 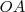 , de modo que
, de modo que
![S = \left[ \frac{n(n+1)}{2} \right]^2 \;\;\;\;\;\;\;\;\;\; (I) S = \left[ \frac{n(n+1)}{2} \right]^2 \;\;\;\;\;\;\;\;\;\; (I)](/latexrender/pictures/ef1e8ba07673690d2ed033da1ee52ff1.png)
 , indicadas na figura:
, indicadas na figura:
 ? Essa região pode ser dividida em dois retângulos, como na figura. Assim
? Essa região pode ser dividida em dois retângulos, como na figura. Assim![L_n = n \left[ \frac{n(n+1)}{2} \right] + n \left[ \frac{(n-1)n}{2} \right] L_n = n \left[ \frac{n(n+1)}{2} \right] + n \left[ \frac{(n-1)n}{2} \right]](/latexrender/pictures/dc5e67880aa252f02d42941ed68fe34a.png)
![= \frac12 n^2 \left[ (n+1)+(n-1) \right] = n^3 = \frac12 n^2 \left[ (n+1)+(n-1) \right] = n^3](/latexrender/pictures/498ab8afa9df2fb164437055465b4ad7.png)

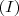 e
e 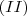 temos
temos![1^3 + 2^3 + \cdots + n^3 = \left[ \frac{n(n+1)}{2} \right]^2 1^3 + 2^3 + \cdots + n^3 = \left[ \frac{n(n+1)}{2} \right]^2](/latexrender/pictures/0bd14a9561c0c92449b75c5655e22aa0.png)
 } e B = {
} e B = { }, então o número de elementos A
}, então o número de elementos A  B é:
B é: