 por apotema2010 » Dom Abr 17, 2011 10:23
por apotema2010 » Dom Abr 17, 2011 10:23
O enunciado:
Resolva os sistema abaixo por, pelo menos dois métodos diferentes:
3x+2y-z=0
5x+z=2
2y-3z=7
pelo método de Gauss o resultado que eu cheguei foi x=0,77 y=4,09 e z=5,86
já pelo método de Cramer achei x= 1,571 y=5,28 z=5,86
estão os dois errados ou algum deles está certo?
Por favor me ajude a começar a resolução ou mostrar o caminho para eu resolver esse sistema:
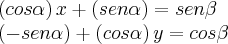
Desde já obrigada.
-
apotema2010
- Usuário Dedicado

-
- Mensagens: 41
- Registrado em: Qua Fev 17, 2010 14:00
- Formação Escolar: GRADUAÇÃO
- Área/Curso: matemática
- Andamento: cursando
 por Molina » Dom Abr 17, 2011 17:50
por Molina » Dom Abr 17, 2011 17:50
Boa tarde.
apotema2010 escreveu:O enunciado:
Resolva os sistema abaixo por, pelo menos dois métodos diferentes:
3x+2y-z=0
5x+z=2
2y-3z=7
pelo método de Gauss o resultado que eu cheguei foi x=0,77 y=4,09 e z=5,86
já pelo método de Cramer achei x= 1,571 y=5,28 z=5,86
estão os dois errados ou algum deles está certo?
Nesta questão acima substitua os o valores encontrados no sistema e verifique se está correto ou não.
apotema2010 escreveu:Por favor me ajude a começar a resolução ou mostrar o caminho para eu resolver esse sistema:
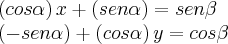
Vamos resolver usando a regra de Cramer:



Concluimos que:
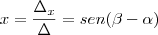


Diego Molina |
CV |
FB |
.COMEquipe AjudaMatemática.com"Existem 10 tipos de pessoas: as que conhecem o sistema binário e as que não conhecem."
-

Molina
- Colaborador Moderador - Professor

-
- Mensagens: 1551
- Registrado em: Dom Jun 01, 2008 14:10
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Licenciatura em Matemática - UFSC
- Andamento: formado
 por apotema2010 » Seg Abr 18, 2011 13:23
por apotema2010 » Seg Abr 18, 2011 13:23
Obrigada pela resolução, vou analisar e ver se tenho dúvidas (talvez tenha).
Abraços.
-
apotema2010
- Usuário Dedicado

-
- Mensagens: 41
- Registrado em: Qua Fev 17, 2010 14:00
- Formação Escolar: GRADUAÇÃO
- Área/Curso: matemática
- Andamento: cursando
 por apotema2010 » Seg Abr 18, 2011 14:15
por apotema2010 » Seg Abr 18, 2011 14:15
Entendi super bem a resolução com as identidades trigonométricas, mas fiz a substituição no primeiro sistema e todas estão erradas, vc pode me ajudar?
-
apotema2010
- Usuário Dedicado

-
- Mensagens: 41
- Registrado em: Qua Fev 17, 2010 14:00
- Formação Escolar: GRADUAÇÃO
- Área/Curso: matemática
- Andamento: cursando
 por Molina » Seg Abr 18, 2011 14:34
por Molina » Seg Abr 18, 2011 14:34
Boa tarde.
apotema2010 escreveu:Entendi super bem a resolução com as identidades trigonométricas, mas fiz a substituição no primeiro sistema e todas estão erradas, vc pode me ajudar?
Tente resolver este sistema por Cramer:
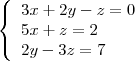
onde:


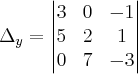
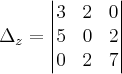
Qualquer dúvida informe!
Diego Molina |
CV |
FB |
.COMEquipe AjudaMatemática.com"Existem 10 tipos de pessoas: as que conhecem o sistema binário e as que não conhecem."
-

Molina
- Colaborador Moderador - Professor

-
- Mensagens: 1551
- Registrado em: Dom Jun 01, 2008 14:10
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Licenciatura em Matemática - UFSC
- Andamento: formado
 por apotema2010 » Seg Abr 18, 2011 14:51
por apotema2010 » Seg Abr 18, 2011 14:51
\Delta=14
\Delta x=22
\Delta y=74
\Delta z=82
x=1,571 y=5,285 z=5,857
se eu substituo esses dados não dá certo
-
apotema2010
- Usuário Dedicado

-
- Mensagens: 41
- Registrado em: Qua Fev 17, 2010 14:00
- Formação Escolar: GRADUAÇÃO
- Área/Curso: matemática
- Andamento: cursando
 por Molina » Seg Abr 18, 2011 19:47
por Molina » Seg Abr 18, 2011 19:47
Diego Molina |
CV |
FB |
.COMEquipe AjudaMatemática.com"Existem 10 tipos de pessoas: as que conhecem o sistema binário e as que não conhecem."
-

Molina
- Colaborador Moderador - Professor

-
- Mensagens: 1551
- Registrado em: Dom Jun 01, 2008 14:10
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Licenciatura em Matemática - UFSC
- Andamento: formado
 por LuizAquino » Seg Abr 18, 2011 20:37
por LuizAquino » Seg Abr 18, 2011 20:37
Olá apotema2010,
Ao que parece você está aproximando a solução.
Ou seja, você está pegando x = 22/14 e efetuando a divisão aproximada de 22 por 14, dizendo assim que a solução é x = 1,571.
É óbvio que se você fizer isso e substituir as aproximações de cada uma das incógnitas nas equações você não encontrará uma igualdade.
Para achar a igualdade você precisa substituir as incógnitas pelo valor certo e não por uma aproximação.
-

LuizAquino
- Colaborador Moderador - Professor

-
- Mensagens: 2654
- Registrado em: Sex Jan 21, 2011 09:11
- Localização: Teófilo Otoni - MG
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Mestrado - Modelagem Computacional
- Andamento: formado
-
 por apotema2010 » Ter Abr 19, 2011 09:42
por apotema2010 » Ter Abr 19, 2011 09:42
Obrigada pela ajuda, errei no sinal e na aproximação, as dicas foram fundamentais para o meu entendimento, abraços.
-
apotema2010
- Usuário Dedicado

-
- Mensagens: 41
- Registrado em: Qua Fev 17, 2010 14:00
- Formação Escolar: GRADUAÇÃO
- Área/Curso: matemática
- Andamento: cursando
Voltar para Matrizes e Determinantes
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- [Raíz da função] Dois métodos com resultados diferentes
por char0 » Qui Mar 15, 2012 00:36
- 2 Respostas
- 1836 Exibições
- Última mensagem por char0

Qui Mar 15, 2012 01:18
Funções
-
- questao resolvida
por adauto martins » Qui Mar 19, 2020 18:54
- 3 Respostas
- 3748 Exibições
- Última mensagem por adauto martins

Dom Abr 05, 2020 11:10
Álgebra Elementar
-
- questao resolvida
por adauto martins » Seg Mai 18, 2020 16:34
- 2 Respostas
- 8292 Exibições
- Última mensagem por adauto martins

Seg Mai 25, 2020 16:34
Cálculo: Limites, Derivadas e Integrais
-
- Integral definida[Resolvida]
por procyon » Ter Nov 01, 2011 00:34
- 3 Respostas
- 3640 Exibições
- Última mensagem por LuizAquino

Ter Nov 01, 2011 22:25
Cálculo: Limites, Derivadas e Integrais
-
- [Limites] analisando os métodos
por Ana_Rodrigues » Qui Fev 02, 2012 18:20
- 2 Respostas
- 1785 Exibições
- Última mensagem por Ana_Rodrigues

Sex Fev 03, 2012 15:06
Cálculo: Limites, Derivadas e Integrais
Usuários navegando neste fórum: Nenhum usuário registrado e 0 visitantes
Assunto:
[Função] do primeiro grau e quadratica
Autor:
Thassya - Sáb Out 01, 2011 16:20
1) Para que os pontos (1,3) e (-3,1) pertençam ao grafico da função f(X)=ax + b ,o valor de b-a deve ser ?
2)Qual o maior valor assumido pela função f : [-7 ,10] em R definida por f(x) = x ao quadrado - 5x + 9?
3) A função f, do primeiro grau, é definida pos f(x)= 3x + k para que o gráfico de f corte o eixo das ordenadas no ponto de ordenada 5 é?
Assunto:
[Função] do primeiro grau e quadratica
Autor:
Neperiano - Sáb Out 01, 2011 19:46
Ola
Qual as suas dúvidas?
O que você não está conseguindo fazer?
Nos mostre para podermos ajudar
Atenciosamente
Assunto:
[Função] do primeiro grau e quadratica
Autor:
joaofonseca - Sáb Out 01, 2011 20:15
1)Dados dois pontos A=(1,3) e B=(-3,1) de uma reta, é possivel definir a sua equação.


Em

substitui-se
m, substitui-se
y e
x por um dos pares ordenados, e resolve-se em ordem a
b.

2)Na equação

não existem zeros.Senão vejamos
Completando o quadrado,

As coordenadas do vertice da parabola são

O eixo de simetria é a reta

.Como se pode observar o vertice está acima do eixo Ox, estando parabola virada para cima, o vertice é um mínimo absoluto.Então basta calcular a função para os valores dos extremos do intervalo.
f(-7)=93
f(10)=59
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
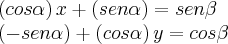





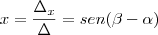



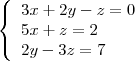


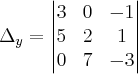
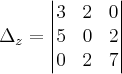




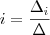 , onde
, onde 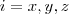


 substitui-se
substitui-se 
 não existem zeros.Senão vejamos
não existem zeros.Senão vejamos

 .Como se pode observar o vertice está acima do eixo Ox, estando parabola virada para cima, o vertice é um mínimo absoluto.Então basta calcular a função para os valores dos extremos do intervalo.
.Como se pode observar o vertice está acima do eixo Ox, estando parabola virada para cima, o vertice é um mínimo absoluto.Então basta calcular a função para os valores dos extremos do intervalo.