 por Raphael Feitas10 » Qui Abr 14, 2011 02:31
por Raphael Feitas10 » Qui Abr 14, 2011 02:31
Repartiu-se 80 bolas entre três meninos,de tal forma que o primeiro recebeu 10 bolas a mais que o segundo,e este 20 bolas a mais que o terceiro.Calcule quantas bolas o primeiro e o segundo receberam juntos.R:70
Brother fiz desse jeito aqui mas ñ conseguie interpreta muito bem essa questão e ñ cheguei na resposta...
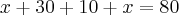
-
Raphael Feitas10
- Colaborador Voluntário

-
- Mensagens: 162
- Registrado em: Ter Jan 04, 2011 20:10
- Formação Escolar: ENSINO MÉDIO
- Área/Curso: Matemática
- Andamento: cursando
 por FilipeCaceres » Qui Abr 14, 2011 10:24
por FilipeCaceres » Qui Abr 14, 2011 10:24
Faça o seguinte,
Chame de x,y,z os meninos, assim temos,
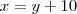
(i)
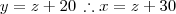
(ii)
E que

(iii)
Agora é só isolar x de (i) e (ii) e substituir em (iii), encontrando o valor de x terá automaticamente os valores de y e z.
Espero que entenda.
-
FilipeCaceres
- Colaborador Voluntário

-
- Mensagens: 351
- Registrado em: Dom Out 31, 2010 21:43
- Formação Escolar: ENSINO MÉDIO PROFISSIONALIZANTE
- Área/Curso: Tec. Mecatrônica
- Andamento: formado
Voltar para Sistemas de Equações
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- números inteiros
por thadeu » Qui Nov 19, 2009 11:41
- 2 Respostas
- 2071 Exibições
- Última mensagem por thadeu

Qui Nov 19, 2009 13:46
Álgebra Elementar
-
- numeros inteiros
por edwilsoncrep » Qui Mar 04, 2010 20:03
- 5 Respostas
- 6391 Exibições
- Última mensagem por adriana_borges

Dom Mai 09, 2010 12:04
Sequências
-
- Numeros inteiros
por Raphael Feitas10 » Qua Jan 05, 2011 00:16
- 3 Respostas
- 2686 Exibições
- Última mensagem por PedroSantos

Qua Jan 05, 2011 19:49
Cálculo: Limites, Derivadas e Integrais
-
- Numeros inteiros
por Raphael Feitas10 » Qui Jan 13, 2011 13:18
- 15 Respostas
- 9704 Exibições
- Última mensagem por Raphael Feitas10

Qua Jan 19, 2011 00:40
Números Complexos
-
- Numeros inteiros 2
por Raphael Feitas10 » Qua Jan 19, 2011 00:28
- 1 Respostas
- 2894 Exibições
- Última mensagem por Renato_RJ

Qua Jan 19, 2011 01:52
Funções
Usuários navegando neste fórum: Nenhum usuário registrado e 0 visitantes
Assunto:
Exercicios de polinomios
Autor:
shaft - Qua Jun 30, 2010 17:30

Então, o exercicio pede para encontrar

.
Bom, tentei resolver a questão acima desenvolvendo as duas partes em ( )...Logo dps cheguei em um resultado q nao soube o q fazer mais.
Se vcs puderem ajudar !
Assunto:
Exercicios de polinomios
Autor:
Douglasm - Qua Jun 30, 2010 17:53
Bom, se desenvolvermos isso, encontramos:

Para que os polinômios sejam iguais, seus respectivos coeficientes devem ser iguais (ax = bx ; ax² = bx², etc.):


Somando a primeira e a segunda equação:

Finalmente:

Até a próxima.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
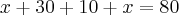

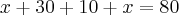

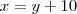 (i)
(i)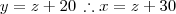 (ii)
(ii) (iii)
(iii)

 .
.



