 por Abelardo » Ter Abr 12, 2011 23:55
por Abelardo » Ter Abr 12, 2011 23:55
Esse dúvida foi retirada do email
''obm-l@mat.puc-rio.br'' e achei interessante, gostaria de ver a opinião de outros. Estou voando demais com isso kkk..
Obs: Sei que
![\sqrt[]{{x}^{2}}=\left|x \right| \sqrt[]{{x}^{2}}=\left|x \right|](/latexrender/pictures/db1caedc7cac55cdeec1fa2040413c52.png)
para todo o número real x e que raiz quadrada de número negativo não está definida no conjuntos dos números reais. Aprendi isso de tanto ver neste fórum kkk!
(-1)^(2/6) = (-1)^(1/3) = -1
'''''No universo dos números reais, qual é o valor correto da potência

? É 1? Ou é -1?
Bem... costumo agir assim:

=
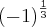
=
![\sqrt[3]{-1} = -1 \sqrt[3]{-1} = -1](/latexrender/pictures/ab94d7a2bd8fc931fd4e098fc8ae5dc2.png)
Procedo assim, pois me parece que a transformação em radical de uma potência com expoente fracionário (e base negativa) só deve ser feita quando o expoente for uma fração irredutível.'''''
Uma outra pessoa apresentou isso também -->
![{(-1)}^{\frac{2}{6}}=(-1)^{\frac{1}{3}}=-1
[(-1)^{2}]^\frac{1}{6}=(1)^\frac{1}{6}=1 {(-1)}^{\frac{2}{6}}=(-1)^{\frac{1}{3}}=-1
[(-1)^{2}]^\frac{1}{6}=(1)^\frac{1}{6}=1](/latexrender/pictures/dad5fc8a5d6d96d975a822ab6de14d59.png)
-

Abelardo
- Colaborador Voluntário

-
- Mensagens: 159
- Registrado em: Qui Mar 03, 2011 01:45
- Formação Escolar: ENSINO MÉDIO
- Andamento: cursando
 por MarceloFantini » Qua Abr 13, 2011 00:42
por MarceloFantini » Qua Abr 13, 2011 00:42
Quando o radicando é negativo, resolvemos o numerador primeiro e depois o denominador do expoente. Acredito que a resposta seja 1.
Futuro MATEMÁTICO
-
MarceloFantini
- Colaborador Moderador

-
- Mensagens: 3126
- Registrado em: Seg Dez 14, 2009 11:41
- Formação Escolar: GRADUAÇÃO
- Andamento: formado
 por FilipeCaceres » Qua Abr 13, 2011 02:15
por FilipeCaceres » Qua Abr 13, 2011 02:15
Para que a resposta seja 1
Acho que o correto seria escrever
![[(-1)^2]^{\frac{1}{^6}}=\sqrt[6]{1}=1 [(-1)^2]^{\frac{1}{^6}}=\sqrt[6]{1}=1](/latexrender/pictures/6ea8a8013775f93f7b5753176b22c39c.png)
mas isso não foi a pergunta inicial.
Mas se o parêntese for apenas para isolar, e é o que eu acredito, então teremos:
![(-1)^{\frac{2}{6}}=(-1)^{\frac{1}{3}}=\sqrt[3]{-1}=-1 (-1)^{\frac{2}{6}}=(-1)^{\frac{1}{3}}=\sqrt[3]{-1}=-1](/latexrender/pictures/edc8bd1cc5bd3153269e4f508730eca0.png)
Abraço.
Editado pela última vez por
FilipeCaceres em Qua Abr 13, 2011 10:45, em um total de 2 vezes.
-
FilipeCaceres
- Colaborador Voluntário

-
- Mensagens: 351
- Registrado em: Dom Out 31, 2010 21:43
- Formação Escolar: ENSINO MÉDIO PROFISSIONALIZANTE
- Área/Curso: Tec. Mecatrônica
- Andamento: formado
 por LuizAquino » Qua Abr 13, 2011 08:54
por LuizAquino » Qua Abr 13, 2011 08:54
Da mesma forma que

é igual a 1, temos que
![\sqrt[6]{(-1)^2} \sqrt[6]{(-1)^2}](/latexrender/pictures/362e175b9649db23f58ea54be5a75665.png)
é igual a 1.
Note que os exemplos acima podem ser reescritos como

e
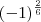
. O detalhe é que primeiro devemos resolver

, para só depois resolver

e
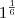
, assim como disse
Fantini.
-

LuizAquino
- Colaborador Moderador - Professor

-
- Mensagens: 2654
- Registrado em: Sex Jan 21, 2011 09:11
- Localização: Teófilo Otoni - MG
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Mestrado - Modelagem Computacional
- Andamento: formado
-
 por FilipeCaceres » Qua Abr 13, 2011 10:20
por FilipeCaceres » Qua Abr 13, 2011 10:20
Quando postei anteriormente estava pensando em outro caso,devemos seguir a ordem
Potenciação ou Radiciação;
Multiplicação ou Divisão;
Adição ou Subtração.
Abraço.
Editado pela última vez por
FilipeCaceres em Qua Abr 13, 2011 10:49, em um total de 1 vez.
-
FilipeCaceres
- Colaborador Voluntário

-
- Mensagens: 351
- Registrado em: Dom Out 31, 2010 21:43
- Formação Escolar: ENSINO MÉDIO PROFISSIONALIZANTE
- Área/Curso: Tec. Mecatrônica
- Andamento: formado
 por FilipeCaceres » Qua Abr 13, 2011 10:39
por FilipeCaceres » Qua Abr 13, 2011 10:39
O caso inicial que ele passou
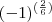
Sendo assim temos
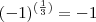
Este é o caso que eu estava me referindo, mas que acabei esquecendo de por os parênteses.
Tendo em mente que as prioridades: parênteses,colchetes,chaves...
Não vejo erro nisso.
Mas no entanto se não tiver estes parênteses concordo plenamente que é 1.
Abraço.
-
FilipeCaceres
- Colaborador Voluntário

-
- Mensagens: 351
- Registrado em: Dom Out 31, 2010 21:43
- Formação Escolar: ENSINO MÉDIO PROFISSIONALIZANTE
- Área/Curso: Tec. Mecatrônica
- Andamento: formado
 por MarceloFantini » Qua Abr 13, 2011 19:31
por MarceloFantini » Qua Abr 13, 2011 19:31
Isto está me lembrando aquela famosa discussão:

? Afinal de contas, dois jeitos de ver:
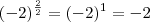
ou

. Qual está certo, aplicar potenciação primeiro ou simplificar expoente? Algo está errado se não tivermos regras fixas. Claro que, podem haver casos onde fazer é equivalente, mas existe um que deve predominar e os outros terão de ser equivalentes a esse para que não haja confusão. Sendo assim, acredito que o dominante seja a potenciação e depois resolvam os outros ou simplifiquem o expoente.
Futuro MATEMÁTICO
-
MarceloFantini
- Colaborador Moderador

-
- Mensagens: 3126
- Registrado em: Seg Dez 14, 2009 11:41
- Formação Escolar: GRADUAÇÃO
- Andamento: formado
 por FilipeCaceres » Qua Abr 13, 2011 19:58
por FilipeCaceres » Qua Abr 13, 2011 19:58
As pessoas se confundem achando que

e não

, pode-se dizer que o "vilão" disso está não fórmula de báskara onde temos o
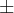
antes da raiz, o que induz as pessoas acreditar que quando tirar
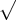
teremos um valor positivo e outro negativo e também pelo fato de que

,por exemplo.
-
FilipeCaceres
- Colaborador Voluntário

-
- Mensagens: 351
- Registrado em: Dom Out 31, 2010 21:43
- Formação Escolar: ENSINO MÉDIO PROFISSIONALIZANTE
- Área/Curso: Tec. Mecatrônica
- Andamento: formado
 por MarceloFantini » Qua Abr 13, 2011 20:10
por MarceloFantini » Qua Abr 13, 2011 20:10
Exatamente. Se
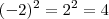
, porque não

? É o mesmo problema. "Ah, mas tem a raíz cúbica." Então se fosse raíz cúbica teria mais de uma solução? Não faz sentido. Portanto, reitero que a resposta deve ser 1.
Editado pela última vez por
MarceloFantini em Qua Abr 13, 2011 20:27, em um total de 1 vez.
Futuro MATEMÁTICO
-
MarceloFantini
- Colaborador Moderador

-
- Mensagens: 3126
- Registrado em: Seg Dez 14, 2009 11:41
- Formação Escolar: GRADUAÇÃO
- Andamento: formado
 por FilipeCaceres » Qua Abr 13, 2011 20:23
por FilipeCaceres » Qua Abr 13, 2011 20:23
Concordo plenamente, a não ser que esteja escrito desta forma
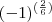
, se for assim, acredito que a resposta será
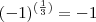
.
Estou certo?
Abraço.
-
FilipeCaceres
- Colaborador Voluntário

-
- Mensagens: 351
- Registrado em: Dom Out 31, 2010 21:43
- Formação Escolar: ENSINO MÉDIO PROFISSIONALIZANTE
- Área/Curso: Tec. Mecatrônica
- Andamento: formado
 por MarceloFantini » Qua Abr 13, 2011 20:27
por MarceloFantini » Qua Abr 13, 2011 20:27
Acredito que não, pois
![(-1)^{\frac{2}{6}} \iff \sqrt[6]{(-1)^2} (-1)^{\frac{2}{6}} \iff \sqrt[6]{(-1)^2}](/latexrender/pictures/4a7d88e636d0bce805bc89d119d4368a.png)
.
Futuro MATEMÁTICO
-
MarceloFantini
- Colaborador Moderador

-
- Mensagens: 3126
- Registrado em: Seg Dez 14, 2009 11:41
- Formação Escolar: GRADUAÇÃO
- Andamento: formado
 por FilipeCaceres » Qua Abr 13, 2011 20:47
por FilipeCaceres » Qua Abr 13, 2011 20:47
Mas assim vc não está considerando os parênteses do
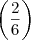
.
Se considerar não teremos
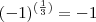
?
-
FilipeCaceres
- Colaborador Voluntário

-
- Mensagens: 351
- Registrado em: Dom Out 31, 2010 21:43
- Formação Escolar: ENSINO MÉDIO PROFISSIONALIZANTE
- Área/Curso: Tec. Mecatrônica
- Andamento: formado
 por MarceloFantini » Qua Abr 13, 2011 20:49
por MarceloFantini » Qua Abr 13, 2011 20:49
Não, não faz diferença os parênteses no expoente. A simplificação não depende de estar entre parênteses ou não.
Futuro MATEMÁTICO
-
MarceloFantini
- Colaborador Moderador

-
- Mensagens: 3126
- Registrado em: Seg Dez 14, 2009 11:41
- Formação Escolar: GRADUAÇÃO
- Andamento: formado
 por joao_pimentel » Qua Dez 14, 2011 20:17
por joao_pimentel » Qua Dez 14, 2011 20:17
Caríssimos
Considerando apenas os números Reais e não os Complexos
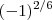
só pode ser -1 e nunca 1
Lembrem-se que
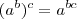
só é válido quando

Assim,

Não tem nada a ver com parentesis como já foi referido, sendo o resultado apenas -1
Cumprimentos
-
joao_pimentel
- Usuário Ativo

-
- Mensagens: 11
- Registrado em: Qua Dez 14, 2011 20:11
- Formação Escolar: GRADUAÇÃO
- Andamento: formado
 por LuizAquino » Qua Dez 14, 2011 21:23
por LuizAquino » Qua Dez 14, 2011 21:23
joao_pimentel escreveu:Considerando apenas os números Reais e não os Complexos
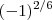
só pode ser -1 e nunca 1
Não. Temos que

.
joao_pimentel escreveu:Lembrem-se que
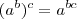
só é válido quando a>0.
Errado. Se
b e
c são números inteiros e
a é um número real não nulo, então a identidade é sempre válida.
Por exemplo, note que:
![\left[(-1)^3\right]^2 = \left[-1\right]^2 = 1 \left[(-1)^3\right]^2 = \left[-1\right]^2 = 1](/latexrender/pictures/16ccf8934fa7153973a81041f555fb8e.png)
Por outro lado, temos que:
![\left[(-1)^3\right]^2 = (-1)^6 = 1 \left[(-1)^3\right]^2 = (-1)^6 = 1](/latexrender/pictures/7d84483cb1543a56465ab2c1bc55b1fc.png)
Entretanto, se
a,
b e
c são números reais, então a identidade é sempre válida apenas quando a > 0.
Isso porque, para a<0, dependendo do valor de b e c a operação pode ser inválida.
Por exemplo, a identidade
![\left[(-1)^3\right]^\frac{1}{2} = (-1)^\frac{3}{2} \left[(-1)^3\right]^\frac{1}{2} = (-1)^\frac{3}{2}](/latexrender/pictures/92be7ff9e25d2df6a3009dab7df06238.png)
é
inválida no conjunto dos reais. Já a identidade
![\left[(-1)^3\right]^\frac{1}{5} = (-1)^\frac{3}{5} \left[(-1)^3\right]^\frac{1}{5} = (-1)^\frac{3}{5}](/latexrender/pictures/612ee55bf77ff1b8ed75b346aded7b6b.png)
é perfeitamente
válida.
-

LuizAquino
- Colaborador Moderador - Professor

-
- Mensagens: 2654
- Registrado em: Sex Jan 21, 2011 09:11
- Localização: Teófilo Otoni - MG
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Mestrado - Modelagem Computacional
- Andamento: formado
-
 por joao_pimentel » Qui Dez 15, 2011 08:28
por joao_pimentel » Qui Dez 15, 2011 08:28
Meu caro. São questões complexas que aqui coloca.
No entanto
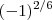
só pode ser

no meu entender
Não sei exatamente qual o domínio da função
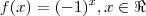
ou mais generalizadamente

ou ainda o domínio bidimensional da função
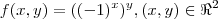
ou ainda

São questões intrigantes, mas continuo a achar que neste caso nada tem a ver com parentesis, pois o expoente e a base resolvem-se sempre de forma independente. Assim neste caso

Cumprimentos
-
joao_pimentel
- Usuário Ativo

-
- Mensagens: 11
- Registrado em: Qua Dez 14, 2011 20:11
- Formação Escolar: GRADUAÇÃO
- Andamento: formado
 por LuizAquino » Qui Dez 15, 2011 09:21
por LuizAquino » Qui Dez 15, 2011 09:21
joao_pimentel escreveu:No entanto
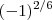
só pode ser -1 no meu entender.
Pela
definição de potenciação com expoente racional, dados
m e
n naturais (com
n não nulo) e
a real temos que:
![a^\frac{m}{n} = \sqrt[n]{a^m} a^\frac{m}{n} = \sqrt[n]{a^m}](/latexrender/pictures/0f147d714af3993847aaa13ec0733c84.png)
, quando a raiz
n-ésima estiver bem definida.
Agora note que:
![(-1)^\frac{2}{6} = \sqrt[6]{(-1)^2} = \sqrt[6]{1} = 1 (-1)^\frac{2}{6} = \sqrt[6]{(-1)^2} = \sqrt[6]{1} = 1](/latexrender/pictures/000ba2a7e1142d5a7476fcda763893d7.png)
-

LuizAquino
- Colaborador Moderador - Professor

-
- Mensagens: 2654
- Registrado em: Sex Jan 21, 2011 09:11
- Localização: Teófilo Otoni - MG
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Mestrado - Modelagem Computacional
- Andamento: formado
-
 por joao_pimentel » Qui Dez 15, 2011 09:28
por joao_pimentel » Qui Dez 15, 2011 09:28
Presumo que tal regra para este expoente só seja válida quando

, pois
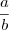
neste caso dá um número racional e não pode resultar da multiplicação de dois inteiros
-
joao_pimentel
- Usuário Ativo

-
- Mensagens: 11
- Registrado em: Qua Dez 14, 2011 20:11
- Formação Escolar: GRADUAÇÃO
- Andamento: formado
 por fraol » Dom Fev 12, 2012 11:53
por fraol » Dom Fev 12, 2012 11:53
Que intrigante essa questão!
Nessa discussão temos dois resultados distintos:
![(-1)^\frac{2}{6} = (-1)^\frac{1}{3} = \sqrt[3]{-1} = -1 (-1)^\frac{2}{6} = (-1)^\frac{1}{3} = \sqrt[3]{-1} = -1](/latexrender/pictures/4d423009dc1966f274b926df345c4056.png)
e
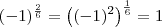
Logo tem algo errado aí.
Isso nos faz considerar a expressão
expoente racional na forma irredutível para a definição desse tipo de potenciação.
Se assim não for, no corpo dos números reais, estaríamos aceitando que:
![(-1)^\frac{2}{6} = \left( (-1)^\frac{1}{6} \right)^2 = 1 = (\sqrt[6]{-1})^2 (-1)^\frac{2}{6} = \left( (-1)^\frac{1}{6} \right)^2 = 1 = (\sqrt[6]{-1})^2](/latexrender/pictures/cd3918ebceaf1abe83a0df7f2071980e.png)
. Mas
![\sqrt[6]{-1} \sqrt[6]{-1}](/latexrender/pictures/870ec2eabd0cf1ba5c196a61103baeac.png)
não é um número real.
-
fraol
- Colaborador Voluntário

-
- Mensagens: 392
- Registrado em: Dom Dez 11, 2011 20:08
- Localização: Mogi das Cruzes-SP
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Matemática
- Andamento: formado
 por LuizAquino » Dom Fev 12, 2012 12:22
por LuizAquino » Dom Fev 12, 2012 12:22
fraol escreveu:Isso nos faz considerar a expressão
expoente racional na forma irredutível para a definição desse tipo de potenciação.
Se assim não for, no corpo dos números reais, estaríamos aceitando que:
![(-1)^\frac{2}{6} = \left( (-1)^\frac{1}{6} \right)^2 = 1 = (\sqrt[6]{-1})^2 (-1)^\frac{2}{6} = \left( (-1)^\frac{1}{6} \right)^2 = 1 = (\sqrt[6]{-1})^2](/latexrender/pictures/cd3918ebceaf1abe83a0df7f2071980e.png)
. Mas
![\sqrt[6]{-1} \sqrt[6]{-1}](/latexrender/pictures/870ec2eabd0cf1ba5c196a61103baeac.png)
não é um número real.
Essa argumentação não procede, pois não se poderia fazer essa primeira passagem
![(-1)^\frac{2}{6} = \left[ (-1)^\frac{1}{6} \right]^2 (-1)^\frac{2}{6} = \left[ (-1)^\frac{1}{6} \right]^2](/latexrender/pictures/a45bd628f0416abf55e3812ad1bd9e75.png)
no conjunto dos reais.
Ou seja, considerando o conjunto dos reais e sendo m e n inteiros (com n não nulo), temos que

,
apenas quando faz sentido calcular

no conjunto dos reais.
-

LuizAquino
- Colaborador Moderador - Professor

-
- Mensagens: 2654
- Registrado em: Sex Jan 21, 2011 09:11
- Localização: Teófilo Otoni - MG
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Mestrado - Modelagem Computacional
- Andamento: formado
-
 por fraol » Seg Fev 13, 2012 23:21
por fraol » Seg Fev 13, 2012 23:21
Professor LuizAquino,
Antes de mais nada quero declarar que sou fã da sua matemática aqui no forum,
aprendo e reaprendo muito com as suas intervenções e gosto também daquele
bordão final "Agora termine o exercício".
Bom, retomei essa questão estar convicto que a resposta correta desse caso é -1.
Aliás, executei a expressão no Sage, wxMaxima, no Geogebra, no WolframAlpha,
na calculadora do Google, etc. e o resultado é -1.
Alguns colegas aqui do forum advogam que a resposta é 1, usando o argumento que

,
então, também é verdade que

e, claramente,
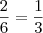
.
Como não podemos ter duas respostas distintas para um mesmo problema,
exceto em casos de aproximações, há que se recorrer a uma regra,
ou exceção de regra, que "regule" o assunto.
Minha conjectura a respeito é que em primeiro lugar
devemos simplificar o expoente, torná-lo uma fração irredutível.
Depois disso aplicamos as propriedades operatórias das potências
com expoente fracionário discutidas nas postagens acima. Aí incluídos
os casos da falta de sentido das raízes com radicando negativo e índice par.
Em outras palavras, estamos dizendo a mesma coisa mas
Em outras palavras.
Abraço.
-
fraol
- Colaborador Voluntário

-
- Mensagens: 392
- Registrado em: Dom Dez 11, 2011 20:08
- Localização: Mogi das Cruzes-SP
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Matemática
- Andamento: formado
 por MarceloFantini » Seg Fev 13, 2012 23:30
por MarceloFantini » Seg Fev 13, 2012 23:30
Fraol, neste caso não é uma simples multiplicação de números, a ordem dos fatores é de importância fundamental. Veja que no wolfram a resposta é um imaginário:
http://www.wolframalpha.com/input/?i=%2 ... 282%2F6%29Futuro MATEMÁTICO
-
MarceloFantini
- Colaborador Moderador

-
- Mensagens: 3126
- Registrado em: Seg Dez 14, 2009 11:41
- Formação Escolar: GRADUAÇÃO
- Andamento: formado
 por fraol » Seg Fev 13, 2012 23:44
por fraol » Seg Fev 13, 2012 23:44
Oi MarceloFantini,
Sim, de fato é um número imaginário no qual uma das raízes, a real, é -1.
Quero que desculpem a insistência, a polemização. Meu intuito é dirimir dúvidas, inclusive as minhas.
-
fraol
- Colaborador Voluntário

-
- Mensagens: 392
- Registrado em: Dom Dez 11, 2011 20:08
- Localização: Mogi das Cruzes-SP
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Matemática
- Andamento: formado
 por MarceloFantini » Seg Fev 13, 2012 23:51
por MarceloFantini » Seg Fev 13, 2012 23:51
Sem problemas. É verdade o que você falou sobre
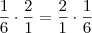
, mas isto não é verdade quando tomamos como potências. Este é um caso de
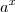
com

apenas, em particular,

. A função exponencial complexa não preserva ordem e também em geral não é válido a propriedade que

.
Futuro MATEMÁTICO
-
MarceloFantini
- Colaborador Moderador

-
- Mensagens: 3126
- Registrado em: Seg Dez 14, 2009 11:41
- Formação Escolar: GRADUAÇÃO
- Andamento: formado
 por LuizAquino » Ter Fev 14, 2012 01:38
por LuizAquino » Ter Fev 14, 2012 01:38
fraol escreveu:Antes de mais nada quero declarar que sou fã da sua matemática aqui no forum,
aprendo e reaprendo muito com as suas intervenções e gosto também daquele
bordão final "Agora termine o exercício".
Todos nós aprendemos muito aqui no fórum! É um ótimo espaço para trocarmos ideias!
Quando ao "bordão", é aquela velha história: o nosso objetivo básico aqui no fórum é tirar dúvidas e apontar os caminhos, não apenas resolver um exercício.
fraol escreveu:Bom, retomei essa questão estar convicto que a resposta correta desse caso é -1.
Aliás, executei a expressão no Sage, wxMaxima, no Geogebra, no WolframAlpha,
na calculadora do Google, etc. e o resultado é -1.
Na grande parte dos programas que você executar (-1)^(2/6) ele irá fazer o que foi programado nele: primeiro resolver a operação de divisão que aparece no expoente para só depois calcular a potenciação. Ele não fará qualquer análise em relação as propriedades de radiciação.
Vejamos novamente a seguinte propriedade de radiciação:
![\sqrt[n]{a^m} = a^{\frac{m}{n}} \sqrt[n]{a^m} = a^{\frac{m}{n}}](/latexrender/pictures/cdd70cbc67c0c3af89bbc72fa204239d.png)
Agora note que podemos escrever sem qualquer problema o seguinte radical:
![\sqrt[6]{(-1)^2} \sqrt[6]{(-1)^2}](/latexrender/pictures/362e175b9649db23f58ea54be5a75665.png)
Mas que operação devemos fazer primeiro? A radiciação ou a potenciação?
Ora, sabemos que é a potenciação, para só depois a radiciação. Primeiro calculamos

e de seu resultado calculamos a raiz sexta.
Agora usando a propriedade citada acima, aquela operação pode ser reescrita como:
![\sqrt[6]{(-1)^2} = (-1)^\frac{2}{6} \sqrt[6]{(-1)^2} = (-1)^\frac{2}{6}](/latexrender/pictures/24fcf96db9ff9793122e3675cc7cfacb.png)
Para essa identidade fazer sentido, ambos os lados da equação precisam assumir o mesmo valor.
Devemos então calcular
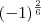
assim como fizemos antes: primeiro calculamos

e de seu resultado calculamos a raiz sexta. Em outras palavras, faremos:
![(-1)^{\frac{2}{6}} = \left[(-1)^2\right]^{\frac{1}{6}} = \sqrt[6]{(-1)^2} (-1)^{\frac{2}{6}} = \left[(-1)^2\right]^{\frac{1}{6}} = \sqrt[6]{(-1)^2}](/latexrender/pictures/ccae14fe3ebdea371d88289a63a8f36f.png)
-

LuizAquino
- Colaborador Moderador - Professor

-
- Mensagens: 2654
- Registrado em: Sex Jan 21, 2011 09:11
- Localização: Teófilo Otoni - MG
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Mestrado - Modelagem Computacional
- Andamento: formado
-
 por timoteo » Ter Fev 14, 2012 08:14
por timoteo » Ter Fev 14, 2012 08:14
valor de (-1)^2/6.
bem, dei uma olhada no que foi dito e achei interessante as respostas. Gostaria de dizer que ao darem as respostas vcs tem que demonstrar o caminho que fizeram!
vamos la, eu fiz assim: (-1)^2/6 = (-1)^1/6 x (-1)^1/6 =
![\sqrt[6]{(-1)^{1}}\sqrt[6]{(-1)^{1}}{\equiv}\sqrt[6]{(-1)}^{1}{(-1)}^{1}\Leftrightarrow \sqrt[6]{(-1)}^{2} \sqrt[6]{(-1)^{1}}\sqrt[6]{(-1)^{1}}{\equiv}\sqrt[6]{(-1)}^{1}{(-1)}^{1}\Leftrightarrow \sqrt[6]{(-1)}^{2}](/latexrender/pictures/2021beaddfab806b686d685c9b0b1da9.png)
. como sabemos
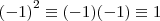
como viram, se fizermos o caminho inverso, sem cortar resultados que achamos irrelevantes, chegamos a essa resposta.
espero ter ajudado, logo trarei um problema que quero a ajuda de todos!
-
timoteo
- Colaborador Voluntário

-
- Mensagens: 117
- Registrado em: Ter Fev 14, 2012 07:07
- Formação Escolar: GRADUAÇÃO
- Área/Curso: bacharel matemática
- Andamento: cursando
 por joao_pimentel » Ter Fev 14, 2012 08:36
por joao_pimentel » Ter Fev 14, 2012 08:36
Mais entropia

Eu discordo de todos vós
Eu acho que
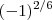
nem é 1, nem -1, é um número complexo. Ora vejam:

Então!!!???
-
joao_pimentel
- Usuário Ativo

-
- Mensagens: 11
- Registrado em: Qua Dez 14, 2011 20:11
- Formação Escolar: GRADUAÇÃO
- Andamento: formado
 por timoteo » Ter Fev 14, 2012 15:48
por timoteo » Ter Fev 14, 2012 15:48
eu estava observando a minha demonstraçao e encontrei um erro.
quando eu fiz:
![\sqrt[6]{(-1)} \sqrt[6]{(-1)} \sqrt[6]{(-1)} \sqrt[6]{(-1)}](/latexrender/pictures/b06173c48bd22d5a1f9be0025ff13dc9.png)
= 1 ha um erro, pois quando o expoente é par e a base negativa, nao ha resoluçao no conjunto dos reais, vejamos:
![\sqrt[2n]{-a} \equiv x \sqrt[2n]{-a} \equiv x](/latexrender/pictures/8eb21cc2303c067420a45b4e7a90a13f.png)
entao

,mas como sabemos todo numero real elevado ao quadrado é positivo.
isto posto, lamento informar que concordo com a resposta de Joao pimentel.
Editado pela última vez por
timoteo em Ter Fev 14, 2012 16:32, em um total de 1 vez.
-
timoteo
- Colaborador Voluntário

-
- Mensagens: 117
- Registrado em: Ter Fev 14, 2012 07:07
- Formação Escolar: GRADUAÇÃO
- Área/Curso: bacharel matemática
- Andamento: cursando
 por MarceloFantini » Ter Fev 14, 2012 16:26
por MarceloFantini » Ter Fev 14, 2012 16:26

Para mim o raciocínio é análogo. Não podemos efetuar a radiciação primeiro, e sim a
potenciação.
Futuro MATEMÁTICO
-
MarceloFantini
- Colaborador Moderador

-
- Mensagens: 3126
- Registrado em: Seg Dez 14, 2009 11:41
- Formação Escolar: GRADUAÇÃO
- Andamento: formado
Voltar para Álgebra Elementar
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Qual o valor de K?
por Talvane Ramos » Ter Mar 23, 2010 13:12
- 2 Respostas
- 4483 Exibições
- Última mensagem por joao_pimentel

Qua Dez 14, 2011 20:21
Sistemas de Equações
-
- Qual é o valor de m
por andersontricordiano » Ter Mai 10, 2011 21:58
- 2 Respostas
- 1994 Exibições
- Última mensagem por DanielRJ

Ter Mai 10, 2011 22:32
Funções
-
- qual é o valor de x na equação:
por aninha1701 » Qui Mar 12, 2009 11:56
- 2 Respostas
- 7294 Exibições
- Última mensagem por Molina

Qui Mar 12, 2009 17:38
Logaritmos
-
- Limite-Qual o Valor de a?
por Luthius » Sex Jul 31, 2009 11:19
- 13 Respostas
- 11526 Exibições
- Última mensagem por Elcioschin

Seg Ago 03, 2009 19:02
Cálculo: Limites, Derivadas e Integrais
-
- Qual o valor recebido?
por Leone de Paula » Qua Jun 16, 2010 22:27
- 2 Respostas
- 1702 Exibições
- Última mensagem por Leone de Paula

Qui Jun 17, 2010 16:17
Progressões
Usuários navegando neste fórum: Nenhum usuário registrado e 0 visitantes
Assunto:
Princípio da Indução Finita
Autor:
Fontelles - Dom Jan 17, 2010 14:42
Não sei onde este tópico se encaixaria. Então me desculpem.
Eu não entendi essa passagem, alguém pode me explicar?

O livro explica da seguinte forma.
1°) P(1) é verdadeira, pois

2°) Admitamos que

, seja verdadeira:

(hipótese da indução)
e provemos que

Temos: (Nessa parte)

Assunto:
Princípio da Indução Finita
Autor:
MarceloFantini - Seg Jan 18, 2010 01:55
Boa noite Fontelles.
Não sei se você está familiarizado com o
Princípio da Indução Finita, portanto vou tentar explicar aqui.
Ele dá uma equação, no caso:

E pergunta: ela vale para todo n? Como proceder: no primeiro passo, vemos se existe pelo menos um caso na qual ela é verdadeira:

Portanto, existe pelo menos um caso para o qual ela é verdadeira. Agora, supomos que

seja verdadeiro, e pretendemos provar que também é verdadeiro para

.




Daí pra frente, ele usou o primeiro membro para chegar em uma conclusão que validava a tese. Lembre-se: nunca saia da tese.
Espero ter ajudado.
Um abraço.
Assunto:
Princípio da Indução Finita
Autor:
Fontelles - Seg Jan 18, 2010 02:28
Mas, Fantini, ainda fiquei em dúvida na passagem que o autor fez (deixei uma msg entre o parêntese).
Obrigado pela ajuda, mesmo assim.
Abraço!
Assunto:
Princípio da Indução Finita
Autor:
Fontelles - Qui Jan 21, 2010 11:32
Galera, ajuda aí!
Por falar nisso, alguém conhece algum bom material sobre o assunto. O livro do Iezzi, Matemática Elementar vol. 1 não está tão bom.
Assunto:
Princípio da Indução Finita
Autor:
MarceloFantini - Qui Jan 21, 2010 12:25
Boa tarde Fontelles!
Ainda não estou certo de qual é a sua dúvida, mas tentarei novamente.
O que temos que provar é isso:

, certo? O autor começou do primeiro membro:

Isso é verdadeiro, certo? Ele apenas aplicou a distributiva. Depois, partiu para uma desigualdade:

Que é outra verdade. Agora, com certeza:

Agora, como

é

a

, e este por sua vez é sempre

que

, logo:

Inclusive, nunca é igual, sempre maior.
Espero (dessa vez) ter ajudado.
Um abraço.
Assunto:
Princípio da Indução Finita
Autor:
Caeros - Dom Out 31, 2010 10:39
Por curiosidade estava estudando indução finita e ao analisar a questão realmente utilizar a desigualdade apresentada foi uma grande sacada para este problema, só queria tirar uma dúvida sobre a sigla (c.q.d), o que significa mesmo?
Assunto:
Princípio da Indução Finita
Autor:
andrefahl - Dom Out 31, 2010 11:37
c.q.d. = como queriamos demonstrar =)
Assunto:
Princípio da Indução Finita
Autor:
Abelardo - Qui Mai 05, 2011 17:33
Fontelles, um bom livro para quem ainda está ''pegando'' o assunto é:'' Manual de Indução Matemática - Luís Lopes''. É baratinho e encontras na net com facilidade. Procura também no site da OBM, vais encontrar com facilidade material sobre PIF... em alguns sites que preparam alunos para colégios militares em geral também tem excelentes materiais.
Assunto:
Princípio da Indução Finita
Autor:
MarceloFantini - Qui Mai 05, 2011 20:05
Abelardo, faz 1 ano que o Fontelles não visita o site, da próxima vez verifique as datas.
Assunto:
Princípio da Indução Finita
Autor:
Vennom - Qui Abr 26, 2012 23:04
MarceloFantini escreveu:Abelardo, faz 1 ano que o Fontelles não visita o site, da próxima vez verifique as datas.
Rpz, faz um ano que o fulano não visita o site, mas ler esse comentário dele enquanto respondia a outro tópico me ajudou. hAUEhUAEhUAEH obrigado, Marcelo. Sua explicação de indução finita me sanou uma dúvida sobre outra coisa.

Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
![\sqrt[]{{x}^{2}}=\left|x \right| \sqrt[]{{x}^{2}}=\left|x \right|](/latexrender/pictures/db1caedc7cac55cdeec1fa2040413c52.png) para todo o número real x e que raiz quadrada de número negativo não está definida no conjuntos dos números reais. Aprendi isso de tanto ver neste fórum kkk!
para todo o número real x e que raiz quadrada de número negativo não está definida no conjuntos dos números reais. Aprendi isso de tanto ver neste fórum kkk! ? É 1? Ou é -1?
? É 1? Ou é -1? =
= 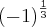 =
= ![\sqrt[3]{-1} = -1 \sqrt[3]{-1} = -1](/latexrender/pictures/ab94d7a2bd8fc931fd4e098fc8ae5dc2.png)
![{(-1)}^{\frac{2}{6}}=(-1)^{\frac{1}{3}}=-1
[(-1)^{2}]^\frac{1}{6}=(1)^\frac{1}{6}=1 {(-1)}^{\frac{2}{6}}=(-1)^{\frac{1}{3}}=-1
[(-1)^{2}]^\frac{1}{6}=(1)^\frac{1}{6}=1](/latexrender/pictures/dad5fc8a5d6d96d975a822ab6de14d59.png)




![[(-1)^2]^{\frac{1}{^6}}=\sqrt[6]{1}=1 [(-1)^2]^{\frac{1}{^6}}=\sqrt[6]{1}=1](/latexrender/pictures/6ea8a8013775f93f7b5753176b22c39c.png) mas isso não foi a pergunta inicial.
mas isso não foi a pergunta inicial.![(-1)^{\frac{2}{6}}=(-1)^{\frac{1}{3}}=\sqrt[3]{-1}=-1 (-1)^{\frac{2}{6}}=(-1)^{\frac{1}{3}}=\sqrt[3]{-1}=-1](/latexrender/pictures/edc8bd1cc5bd3153269e4f508730eca0.png)
 é igual a 1, temos que
é igual a 1, temos que ![\sqrt[6]{(-1)^2} \sqrt[6]{(-1)^2}](/latexrender/pictures/362e175b9649db23f58ea54be5a75665.png) é igual a 1.
é igual a 1. e
e 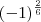 . O detalhe é que primeiro devemos resolver
. O detalhe é que primeiro devemos resolver  , para só depois resolver
, para só depois resolver  e
e 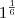 , assim como disse
, assim como disse 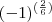
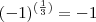
 ? Afinal de contas, dois jeitos de ver:
? Afinal de contas, dois jeitos de ver: 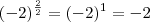 ou
ou  . Qual está certo, aplicar potenciação primeiro ou simplificar expoente? Algo está errado se não tivermos regras fixas. Claro que, podem haver casos onde fazer é equivalente, mas existe um que deve predominar e os outros terão de ser equivalentes a esse para que não haja confusão. Sendo assim, acredito que o dominante seja a potenciação e depois resolvam os outros ou simplifiquem o expoente.
. Qual está certo, aplicar potenciação primeiro ou simplificar expoente? Algo está errado se não tivermos regras fixas. Claro que, podem haver casos onde fazer é equivalente, mas existe um que deve predominar e os outros terão de ser equivalentes a esse para que não haja confusão. Sendo assim, acredito que o dominante seja a potenciação e depois resolvam os outros ou simplifiquem o expoente. e não
e não  , pode-se dizer que o "vilão" disso está não fórmula de báskara onde temos o
, pode-se dizer que o "vilão" disso está não fórmula de báskara onde temos o 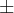 antes da raiz, o que induz as pessoas acreditar que quando tirar
antes da raiz, o que induz as pessoas acreditar que quando tirar 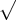 teremos um valor positivo e outro negativo e também pelo fato de que
teremos um valor positivo e outro negativo e também pelo fato de que  ,por exemplo.
,por exemplo.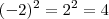 , porque não
, porque não  ? É o mesmo problema. "Ah, mas tem a raíz cúbica." Então se fosse raíz cúbica teria mais de uma solução? Não faz sentido. Portanto, reitero que a resposta deve ser 1.
? É o mesmo problema. "Ah, mas tem a raíz cúbica." Então se fosse raíz cúbica teria mais de uma solução? Não faz sentido. Portanto, reitero que a resposta deve ser 1.![(-1)^{\frac{2}{6}} \iff \sqrt[6]{(-1)^2} (-1)^{\frac{2}{6}} \iff \sqrt[6]{(-1)^2}](/latexrender/pictures/4a7d88e636d0bce805bc89d119d4368a.png) .
.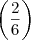 .
.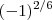 só pode ser -1 e nunca 1
só pode ser -1 e nunca 1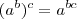 só é válido quando
só é válido quando 


 .
.![\left[(-1)^3\right]^2 = \left[-1\right]^2 = 1 \left[(-1)^3\right]^2 = \left[-1\right]^2 = 1](/latexrender/pictures/16ccf8934fa7153973a81041f555fb8e.png)
![\left[(-1)^3\right]^2 = (-1)^6 = 1 \left[(-1)^3\right]^2 = (-1)^6 = 1](/latexrender/pictures/7d84483cb1543a56465ab2c1bc55b1fc.png)
![\left[(-1)^3\right]^\frac{1}{2} = (-1)^\frac{3}{2} \left[(-1)^3\right]^\frac{1}{2} = (-1)^\frac{3}{2}](/latexrender/pictures/92be7ff9e25d2df6a3009dab7df06238.png) é
é ![\left[(-1)^3\right]^\frac{1}{5} = (-1)^\frac{3}{5} \left[(-1)^3\right]^\frac{1}{5} = (-1)^\frac{3}{5}](/latexrender/pictures/612ee55bf77ff1b8ed75b346aded7b6b.png) é perfeitamente
é perfeitamente  no meu entender
no meu entender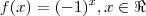 ou mais generalizadamente
ou mais generalizadamente  ou ainda o domínio bidimensional da função
ou ainda o domínio bidimensional da função 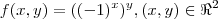 ou ainda
ou ainda 
![a^\frac{m}{n} = \sqrt[n]{a^m} a^\frac{m}{n} = \sqrt[n]{a^m}](/latexrender/pictures/0f147d714af3993847aaa13ec0733c84.png) , quando a raiz
, quando a raiz ![(-1)^\frac{2}{6} = \sqrt[6]{(-1)^2} = \sqrt[6]{1} = 1 (-1)^\frac{2}{6} = \sqrt[6]{(-1)^2} = \sqrt[6]{1} = 1](/latexrender/pictures/000ba2a7e1142d5a7476fcda763893d7.png)
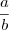 neste caso dá um número racional e não pode resultar da multiplicação de dois inteiros
neste caso dá um número racional e não pode resultar da multiplicação de dois inteiros![(-1)^\frac{2}{6} = (-1)^\frac{1}{3} = \sqrt[3]{-1} = -1 (-1)^\frac{2}{6} = (-1)^\frac{1}{3} = \sqrt[3]{-1} = -1](/latexrender/pictures/4d423009dc1966f274b926df345c4056.png)
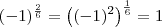
![(-1)^\frac{2}{6} = \left( (-1)^\frac{1}{6} \right)^2 = 1 = (\sqrt[6]{-1})^2 (-1)^\frac{2}{6} = \left( (-1)^\frac{1}{6} \right)^2 = 1 = (\sqrt[6]{-1})^2](/latexrender/pictures/cd3918ebceaf1abe83a0df7f2071980e.png) . Mas
. Mas ![\sqrt[6]{-1} \sqrt[6]{-1}](/latexrender/pictures/870ec2eabd0cf1ba5c196a61103baeac.png) não é um número real.
não é um número real.![(-1)^\frac{2}{6} = \left[ (-1)^\frac{1}{6} \right]^2 (-1)^\frac{2}{6} = \left[ (-1)^\frac{1}{6} \right]^2](/latexrender/pictures/a45bd628f0416abf55e3812ad1bd9e75.png) no conjunto dos reais.
no conjunto dos reais. ,
,  no conjunto dos reais.
no conjunto dos reais. ,
,  e, claramente,
e, claramente, 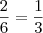 .
.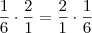 , mas isto não é verdade quando tomamos como potências. Este é um caso de
, mas isto não é verdade quando tomamos como potências. Este é um caso de 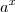 com
com  apenas, em particular,
apenas, em particular,  . A função exponencial complexa não preserva ordem e também em geral não é válido a propriedade que
. A função exponencial complexa não preserva ordem e também em geral não é válido a propriedade que  .
.![\sqrt[n]{a^m} = a^{\frac{m}{n}} \sqrt[n]{a^m} = a^{\frac{m}{n}}](/latexrender/pictures/cdd70cbc67c0c3af89bbc72fa204239d.png)
![\sqrt[6]{(-1)^2} = (-1)^\frac{2}{6} \sqrt[6]{(-1)^2} = (-1)^\frac{2}{6}](/latexrender/pictures/24fcf96db9ff9793122e3675cc7cfacb.png)
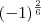 assim como fizemos antes: primeiro calculamos
assim como fizemos antes: primeiro calculamos ![(-1)^{\frac{2}{6}} = \left[(-1)^2\right]^{\frac{1}{6}} = \sqrt[6]{(-1)^2} (-1)^{\frac{2}{6}} = \left[(-1)^2\right]^{\frac{1}{6}} = \sqrt[6]{(-1)^2}](/latexrender/pictures/ccae14fe3ebdea371d88289a63a8f36f.png)
![\sqrt[6]{(-1)^{1}}\sqrt[6]{(-1)^{1}}{\equiv}\sqrt[6]{(-1)}^{1}{(-1)}^{1}\Leftrightarrow \sqrt[6]{(-1)}^{2} \sqrt[6]{(-1)^{1}}\sqrt[6]{(-1)^{1}}{\equiv}\sqrt[6]{(-1)}^{1}{(-1)}^{1}\Leftrightarrow \sqrt[6]{(-1)}^{2}](/latexrender/pictures/2021beaddfab806b686d685c9b0b1da9.png) . como sabemos
. como sabemos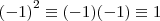


![\sqrt[6]{(-1)} \sqrt[6]{(-1)} \sqrt[6]{(-1)} \sqrt[6]{(-1)}](/latexrender/pictures/b06173c48bd22d5a1f9be0025ff13dc9.png) = 1 ha um erro, pois quando o expoente é par e a base negativa, nao ha resoluçao no conjunto dos reais, vejamos:
= 1 ha um erro, pois quando o expoente é par e a base negativa, nao ha resoluçao no conjunto dos reais, vejamos: ![\sqrt[2n]{-a} \equiv x \sqrt[2n]{-a} \equiv x](/latexrender/pictures/8eb21cc2303c067420a45b4e7a90a13f.png) entao
entao  ,mas como sabemos todo numero real elevado ao quadrado é positivo.
,mas como sabemos todo numero real elevado ao quadrado é positivo.


 , seja verdadeira:
, seja verdadeira: (hipótese da indução)
(hipótese da indução)



 seja verdadeiro, e pretendemos provar que também é verdadeiro para
seja verdadeiro, e pretendemos provar que também é verdadeiro para  .
.





 é
é  a
a  , e este por sua vez é sempre
, e este por sua vez é sempre  que
que  , logo:
, logo:
