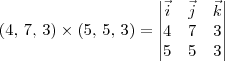Olá, estou postando alguns exercícios que não estou conseguindo resolver totalmente...
Aqui vai mais um:
Dados os vetores a=(3,4,2) e b=(2,1,1), obtenha um vetor que seja ao mesmo tempo ortogonal aos vetores 2a-b e a+b.
2(3,4,2)-(2,1,1)
(6,8,4)-(2,1,1)
(4,7,3)
a+b=(3+2,4+1,2+1)
(5,5,3)
Daqui em diante não sei que direção tomar. Poderiam me dar uma orientação do que preciso começar a fazer?
Um abraço.


 e
e  , por definição temos que o vetor
, por definição temos que o vetor 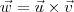 é ortogonal a
é ortogonal a  e
e  .
.