 por andersontricordiano » Seg Abr 11, 2011 15:25
por andersontricordiano » Seg Abr 11, 2011 15:25
Se os números reais positivos x e y forem tais que:
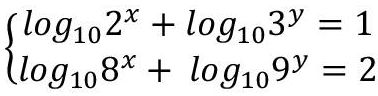
- logxy-Page-1.jpg (12.28 KiB) Exibido 5692 vezes
Então:
Detalhe a resposta é: y=  Agradeço quem resolver e me explicar como se desenvolve esse calculo!
Agradeço quem resolver e me explicar como se desenvolve esse calculo!
Editado pela última vez por
andersontricordiano em Seg Abr 11, 2011 18:07, em um total de 1 vez.
-
andersontricordiano
- Colaborador Voluntário

-
- Mensagens: 192
- Registrado em: Sex Mar 04, 2011 23:02
- Formação Escolar: ENSINO MÉDIO
- Andamento: formado
 por Aliocha Karamazov » Seg Abr 11, 2011 17:54
por Aliocha Karamazov » Seg Abr 11, 2011 17:54
Qual é a pergunta?
-
Aliocha Karamazov
- Usuário Parceiro

-
- Mensagens: 90
- Registrado em: Qua Mar 16, 2011 17:26
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Física
- Andamento: cursando
 por andersontricordiano » Seg Abr 11, 2011 18:09
por andersontricordiano » Seg Abr 11, 2011 18:09
é para descobrir os valores de

e

?
No caso desse exercício a resposta no gabarito está
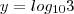
-
andersontricordiano
- Colaborador Voluntário

-
- Mensagens: 192
- Registrado em: Sex Mar 04, 2011 23:02
- Formação Escolar: ENSINO MÉDIO
- Andamento: formado
 por Aliocha Karamazov » Seg Abr 11, 2011 18:32
por Aliocha Karamazov » Seg Abr 11, 2011 18:32
Comece utilizando a seguinte propriedade:
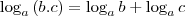
Aí você vai obter um sistema. Tente dividir uma equação pela outra. Mostre suas tentativas.
-
Aliocha Karamazov
- Usuário Parceiro

-
- Mensagens: 90
- Registrado em: Qua Mar 16, 2011 17:26
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Física
- Andamento: cursando
 por andersontricordiano » Seg Abr 11, 2011 20:15
por andersontricordiano » Seg Abr 11, 2011 20:15
Então vai ficar assim no começo do desenvolvimento:

-
andersontricordiano
- Colaborador Voluntário

-
- Mensagens: 192
- Registrado em: Sex Mar 04, 2011 23:02
- Formação Escolar: ENSINO MÉDIO
- Andamento: formado
 por FilipeCaceres » Seg Abr 11, 2011 20:49
por FilipeCaceres » Seg Abr 11, 2011 20:49
Vou lhe dar uma outra dica,
Faz a seguinte substituição,

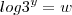
logo,

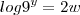
Assim você terá:
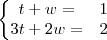
Resolva o sistema que vc encontrará os valores de x e y.
Espero ter ajudado.
Editado pela última vez por
FilipeCaceres em Ter Abr 12, 2011 12:25, em um total de 1 vez.
-
FilipeCaceres
- Colaborador Voluntário

-
- Mensagens: 351
- Registrado em: Dom Out 31, 2010 21:43
- Formação Escolar: ENSINO MÉDIO PROFISSIONALIZANTE
- Área/Curso: Tec. Mecatrônica
- Andamento: formado
 por andersontricordiano » Ter Abr 12, 2011 12:20
por andersontricordiano » Ter Abr 12, 2011 12:20
Eu achei:
w=1 e t = 0
Agora como faço para chegar a resposta
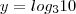
Abraço!
-
andersontricordiano
- Colaborador Voluntário

-
- Mensagens: 192
- Registrado em: Sex Mar 04, 2011 23:02
- Formação Escolar: ENSINO MÉDIO
- Andamento: formado
 por FilipeCaceres » Ter Abr 12, 2011 12:31
por FilipeCaceres » Ter Abr 12, 2011 12:31
Agora você tem,
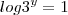
Sabendo que,

Desta forma temos que,
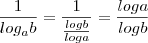
Assim temos,
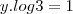

Portanto,
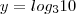
Abraço.
-
FilipeCaceres
- Colaborador Voluntário

-
- Mensagens: 351
- Registrado em: Dom Out 31, 2010 21:43
- Formação Escolar: ENSINO MÉDIO PROFISSIONALIZANTE
- Área/Curso: Tec. Mecatrônica
- Andamento: formado
Voltar para Logaritmos
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Verificar se existem números reais x tais que...
por Aliocha Karamazov » Sex Mar 25, 2011 15:39
- 2 Respostas
- 2033 Exibições
- Última mensagem por Aliocha Karamazov

Sex Mar 25, 2011 15:58
Álgebra Elementar
-
- Números positivos
por plugpc » Qua Mai 20, 2009 19:31
- 3 Respostas
- 2307 Exibições
- Última mensagem por Molina

Qua Mai 20, 2009 22:39
Álgebra Elementar
-
- Números Reais - Simplificar números reais
por ZANGARO » Ter Nov 15, 2011 18:46
- 0 Respostas
- 1946 Exibições
- Última mensagem por ZANGARO

Ter Nov 15, 2011 18:46
Álgebra Elementar
-
- Números reais
por citadp » Dom Jun 24, 2012 16:02
- 1 Respostas
- 1762 Exibições
- Última mensagem por e8group

Dom Jun 24, 2012 19:22
Cálculo: Limites, Derivadas e Integrais
-
- Numeros reais
por vihalmeida » Qui Nov 15, 2012 15:19
- 1 Respostas
- 2202 Exibições
- Última mensagem por DanielFerreira

Qui Nov 15, 2012 18:40
Álgebra Elementar
Usuários navegando neste fórum: Nenhum usuário registrado e 3 visitantes
Assunto:
Unesp - 95 Números Complexos
Autor:
Alucard014 - Dom Ago 01, 2010 18:22
(UNESP - 95) Seja L o Afixo de um Número complexo

em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto.
Assunto:
Unesp - 95 Números Complexos
Autor:
MarceloFantini - Qui Ago 05, 2010 17:27
Seja

o ângulo entre o eixo horizontal e o afixo

. O triângulo é retângulo com catetos

e

, tal que

. Seja

o ângulo complementar. Então

. Como

, o ângulo que o afixo

formará com a horizontal será

, mas negativo pois tem de ser no quarto quadrante. Se

, então

. Como módulo é um:

.
Logo, o afixo é

.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.





 e
e  ?
?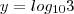

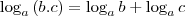




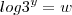

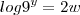
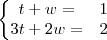

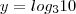

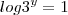

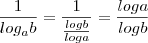
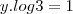

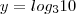

 em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto.
em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto. o ângulo entre o eixo horizontal e o afixo
o ângulo entre o eixo horizontal e o afixo  . O triângulo é retângulo com catetos
. O triângulo é retângulo com catetos  e
e  , tal que
, tal que  . Seja
. Seja  o ângulo complementar. Então
o ângulo complementar. Então  . Como
. Como  , o ângulo que o afixo
, o ângulo que o afixo  formará com a horizontal será
formará com a horizontal será  , mas negativo pois tem de ser no quarto quadrante. Se
, mas negativo pois tem de ser no quarto quadrante. Se  , então
, então  . Como módulo é um:
. Como módulo é um:  .
. .
.