poderiam me ajuda nesses exercicios que ja tentei de toda forma mas noa consegui resolve-los
é sobre matrizes
1-represente explicitamente cada uma das matrizes:
a)A=(aij)2x2 tal que aij=(-1)elevado i+j:
b)A=(aij)3x2 tal que aij={0 se i=j }:
{2i+j se i>j}
{j se i<j}
2-sao dadas as matrizesA=(3),B=(4) e C=(-2).resolva a equaçao "x+2.A(elevado a '' t'')=3.(B+C)(elevado a '' t''):
(2) (1) (1)
3-determine,se existir,a inversa da matriz (2 3)
(4 5):
é a ultima q é a pior de todas nao consegui de nenhum geito fazer
4-se ''A'' e "B" sao matrizes tais que A=(2 1) e B=(1 1 )calcule a matriz y=A(elevado a '' t'') .B:
(1 0) (2 5 )
(-3 1) (0 -1)


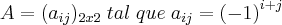
![A=\[
\left(
\begin{array}{ccc}
{a}_{ij} & {a}_{ij} \\
{a}_{ij} & {a}_{ij} \end{array}
\right)\] A=\[
\left(
\begin{array}{ccc}
{a}_{ij} & {a}_{ij} \\
{a}_{ij} & {a}_{ij} \end{array}
\right)\]](/latexrender/pictures/66b8e25dbcade0416c564aa835461b68.png)
 IMPORTANTE: O
IMPORTANTE: O  é o numero da linha e o
é o numero da linha e o 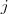 é o numero da coluna:
é o numero da coluna:![A=\[
\left(
\begin{array}{ccc}
{a}_{11} & {a}_{12} \\
{a}_{21} & {a}_{22} \end{array}
\right)\] A=\[
\left(
\begin{array}{ccc}
{a}_{11} & {a}_{12} \\
{a}_{21} & {a}_{22} \end{array}
\right)\]](/latexrender/pictures/a83cd364e4d481ed2da78444b50e8b49.png)
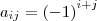 :
:
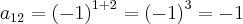
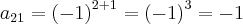

![A=\[
\left(
\begin{array}{ccc}
1 & -1 \\
-1 & 1 \end{array}
\right)\] A=\[
\left(
\begin{array}{ccc}
1 & -1 \\
-1 & 1 \end{array}
\right)\]](/latexrender/pictures/8217b310ddf354499e103a193b8da902.png)
 Bom estudo!
Bom estudo!

 .
.
 :
: