 por Abelardo » Sáb Abr 09, 2011 18:30
por Abelardo » Sáb Abr 09, 2011 18:30
''ITA) ...E tá que tá gostoso!'' Depois desse trocadilho infame, vem a questão.
Considere as seguintes afirmações sobre números reais positivos:
I) Se

e
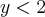
, então
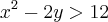
II) Se

ou
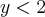
, então
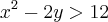
III) Se
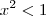
e
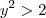
, então
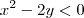
Então, destas é (são) verdadeira(s) ?
O que fiz:
I) Eu assumi na primera questão que y=1 e percebi que x é maior que 3 e menor que 4 e vejo que entra em contradição a afirmação, já que x tem que ser maior que 4. (Falsa)
II) Fiquei na dúvida por causa do conectivo ''ou''.
III) ...
Gostaria de ver uma solução ''mais algébrica'' para os casos, há várias questões que usam desigualdade e ai poderia utilizar o raciocínio de forma semelhante.
-

Abelardo
- Colaborador Voluntário

-
- Mensagens: 159
- Registrado em: Qui Mar 03, 2011 01:45
- Formação Escolar: ENSINO MÉDIO
- Andamento: cursando
 por MarceloFantini » Sáb Abr 09, 2011 20:36
por MarceloFantini » Sáb Abr 09, 2011 20:36
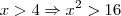

Somando:
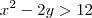
A primeira é verdadeira. Sobre a segunda, eu também diria que é falsa pois o conectivo ou significa que

mas pode ser que
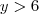
, o que travaria tudo.
Terceira:
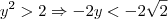
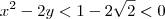
Logo também é verdadeira.
Futuro MATEMÁTICO
-
MarceloFantini
- Colaborador Moderador

-
- Mensagens: 3126
- Registrado em: Seg Dez 14, 2009 11:41
- Formação Escolar: GRADUAÇÃO
- Andamento: formado
 por Abelardo » Sáb Abr 09, 2011 21:28
por Abelardo » Sáb Abr 09, 2011 21:28
Obrigado Fantini, procurarei algumas apostila na net falando sobre as propriedades operatórias das desigualdades.
-

Abelardo
- Colaborador Voluntário

-
- Mensagens: 159
- Registrado em: Qui Mar 03, 2011 01:45
- Formação Escolar: ENSINO MÉDIO
- Andamento: cursando
Voltar para Álgebra Elementar
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
Exercicios de polinomios
Autor:
shaft - Qua Jun 30, 2010 17:30

Então, o exercicio pede para encontrar

.
Bom, tentei resolver a questão acima desenvolvendo as duas partes em ( )...Logo dps cheguei em um resultado q nao soube o q fazer mais.
Se vcs puderem ajudar !
Assunto:
Exercicios de polinomios
Autor:
Douglasm - Qua Jun 30, 2010 17:53
Bom, se desenvolvermos isso, encontramos:

Para que os polinômios sejam iguais, seus respectivos coeficientes devem ser iguais (ax = bx ; ax² = bx², etc.):


Somando a primeira e a segunda equação:

Finalmente:

Até a próxima.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
 e
e 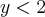 , então
, então 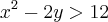
 ou
ou 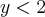 , então
, então 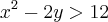
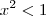 e
e 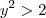 , então
, então 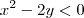


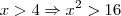

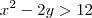
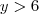 , o que travaria tudo.
, o que travaria tudo.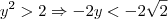
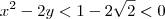



 .
.



