 por Aliocha Karamazov » Qua Abr 06, 2011 19:55
por Aliocha Karamazov » Qua Abr 06, 2011 19:55
Galera, gostaria de uma ajuda aqui:
Resolvendo a desigualdade

obtemos:
Eu tentei fazer da seguinte maneira:
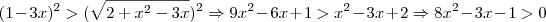
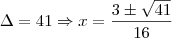
Ainda, pela condição de existência:
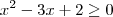
Depois disso, fiz a intersecção com as soluções das duas inequações, mas a resposta saiu diferente do livro. Alguém pode ajudar? Muito obrigado!
-
Aliocha Karamazov
- Usuário Parceiro

-
- Mensagens: 90
- Registrado em: Qua Mar 16, 2011 17:26
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Física
- Andamento: cursando
 por Molina » Qua Abr 06, 2011 20:14
por Molina » Qua Abr 06, 2011 20:14
Boa noite.
A solução da equação

é:
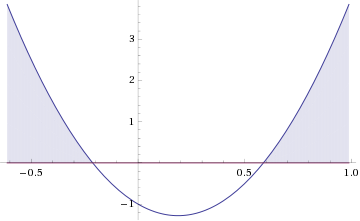
- MSP155619f35i886da6f277000038i2327334091big.gif (6.98 KiB) Exibido 2585 vezes
E a solução de
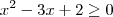
é:

- MSP111019f35iac71ah1eai00005e5c4i2a55f72c8h.gif (6.76 KiB) Exibido 2585 vezes
A interseção dos dois não deu a resposta do livro?
Qual a solução que consta no gabarito?
Diego Molina |
CV |
FB |
.COMEquipe AjudaMatemática.com"Existem 10 tipos de pessoas: as que conhecem o sistema binário e as que não conhecem."
-

Molina
- Colaborador Moderador - Professor

-
- Mensagens: 1551
- Registrado em: Dom Jun 01, 2008 14:10
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Licenciatura em Matemática - UFSC
- Andamento: formado
 por FilipeCaceres » Qua Abr 06, 2011 20:53
por FilipeCaceres » Qua Abr 06, 2011 20:53
Só faltou uma coisinha para vc conseguir resolver.
Vou lhe dar uma dica para um caso genérico.
Para resolver equação do tipo
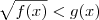
1º Estabeleça o domínio de validade
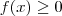
e

(i)
2ºElevando ao quadrado temos,
![f(x)<[g(x)]^2 f(x)<[g(x)]^2](/latexrender/pictures/3a7485117f703accdf37400e64a36348.png)
(ii)
De (i) e (ii) temos
![0\leq f(x)<[g(x)]^2 0\leq f(x)<[g(x)]^2](/latexrender/pictures/6f065d60587f907c025dfa208f3298f9.png)
e

Resumindo
![\sqrt{f(x)}<g(x) \Rightarrow 0\leq f(x)<[g(x)]^2 \sqrt{f(x)}<g(x) \Rightarrow 0\leq f(x)<[g(x)]^2](/latexrender/pictures/ac35d35ac3df282a4ae310adeb55d839.png)
e

Você se esqueceu de fazer

.
Eu encontrei como solução
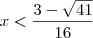
Seria este o valor?
Abraço
-
FilipeCaceres
- Colaborador Voluntário

-
- Mensagens: 351
- Registrado em: Dom Out 31, 2010 21:43
- Formação Escolar: ENSINO MÉDIO PROFISSIONALIZANTE
- Área/Curso: Tec. Mecatrônica
- Andamento: formado
 por Aliocha Karamazov » Qua Abr 06, 2011 23:20
por Aliocha Karamazov » Qua Abr 06, 2011 23:20
Realmente, esse foi o problema: não fiz

. Na minha solução, além de
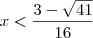
eu havia encontrado

.
Agradeço aos dois que me ajudaram!
-
Aliocha Karamazov
- Usuário Parceiro

-
- Mensagens: 90
- Registrado em: Qua Mar 16, 2011 17:26
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Física
- Andamento: cursando
Voltar para Funções
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Resolvendo indefinição
por barizom » Ter Abr 13, 2010 22:35
- 5 Respostas
- 3625 Exibições
- Última mensagem por barizom

Qui Abr 15, 2010 20:04
Cálculo: Limites, Derivadas e Integrais
-
- Resolvendo Equação Fracionária com MMC
por rapharocket » Qui Mar 03, 2011 16:28
- 0 Respostas
- 2530 Exibições
- Última mensagem por rapharocket

Qui Mar 03, 2011 16:28
Sistemas de Equações
-
- Resolvendo como sistema
por sullivan » Sex Dez 23, 2011 15:27
- 4 Respostas
- 2084 Exibições
- Última mensagem por sullivan

Qua Dez 28, 2011 08:57
Matemática Financeira
-
- Resolvendo equacção do terceiro grau
por jptuga » Sáb Set 17, 2011 06:02
- 2 Respostas
- 1649 Exibições
- Última mensagem por jptuga

Dom Set 18, 2011 08:58
Polinômios
-
- [calculo] Resolvendo esse problema
por amanda s » Sáb Nov 16, 2013 17:21
- 1 Respostas
- 2004 Exibições
- Última mensagem por Pessoa Estranha

Sáb Nov 16, 2013 21:10
Cálculo: Limites, Derivadas e Integrais
Usuários navegando neste fórum: Nenhum usuário registrado e 2 visitantes
Assunto:
Exercicios de polinomios
Autor:
shaft - Qua Jun 30, 2010 17:30

Então, o exercicio pede para encontrar

.
Bom, tentei resolver a questão acima desenvolvendo as duas partes em ( )...Logo dps cheguei em um resultado q nao soube o q fazer mais.
Se vcs puderem ajudar !
Assunto:
Exercicios de polinomios
Autor:
Douglasm - Qua Jun 30, 2010 17:53
Bom, se desenvolvermos isso, encontramos:

Para que os polinômios sejam iguais, seus respectivos coeficientes devem ser iguais (ax = bx ; ax² = bx², etc.):


Somando a primeira e a segunda equação:

Finalmente:

Até a próxima.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
 obtemos:
obtemos: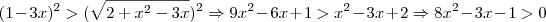
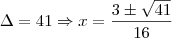
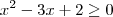


 é:
é: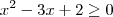 é:
é:
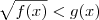
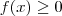 e
e  (i)
(i)![f(x)<[g(x)]^2 f(x)<[g(x)]^2](/latexrender/pictures/3a7485117f703accdf37400e64a36348.png) (ii)
(ii)![0\leq f(x)<[g(x)]^2 0\leq f(x)<[g(x)]^2](/latexrender/pictures/6f065d60587f907c025dfa208f3298f9.png) e
e ![\sqrt{f(x)}<g(x) \Rightarrow 0\leq f(x)<[g(x)]^2 \sqrt{f(x)}<g(x) \Rightarrow 0\leq f(x)<[g(x)]^2](/latexrender/pictures/ac35d35ac3df282a4ae310adeb55d839.png) e
e 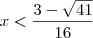

 . Na minha solução, além de
. Na minha solução, além de  .
.
 .
.



