Na reta real, o número 4 está situado entre as raízes de
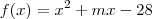 . Nessas condições, os possíveis valores de m são tais que:
. Nessas condições, os possíveis valores de m são tais que:Olhem como eu tentei:
 e
e 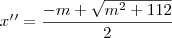
E agora? Tenho que resolver
 e
e 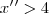 ? A resposta seria a intersecção dos dois? Isso me pareceu estranho. Não tenho certeza se está certo; deve haver uma maneira melhor. Obrigado a todos que puderem ajudar. Abraço!
? A resposta seria a intersecção dos dois? Isso me pareceu estranho. Não tenho certeza se está certo; deve haver uma maneira melhor. Obrigado a todos que puderem ajudar. Abraço!

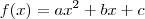 e
e  um valor real que vamos compara com as raízes
um valor real que vamos compara com as raízes 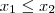
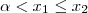 então
então 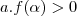
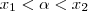 então
então 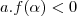
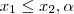 então
então  ou
ou 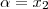 então
então 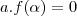
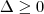 e para 2
e para 2 
 e
e 
 e
e  observe que para qualquer valor de m teremos
observe que para qualquer valor de m teremos 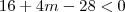
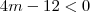

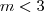 .
.
 em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto.
em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto. . O triângulo é retângulo com catetos
. O triângulo é retângulo com catetos  e
e  , tal que
, tal que  . Seja
. Seja  o ângulo complementar. Então
o ângulo complementar. Então  . Como
. Como  , o ângulo que o afixo
, o ângulo que o afixo  formará com a horizontal será
formará com a horizontal será  , então
, então  . Como módulo é um:
. Como módulo é um:  .
. .
.