 por Juliane » Sáb Abr 02, 2011 20:46
por Juliane » Sáb Abr 02, 2011 20:46
Dados A={x| x é primo e 1
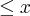
<6}, B={x

Z* | -2,6<x

13/2 }, C={x | x é um numero inteiro, par, não nulo, e menor que 8}

= ?
para
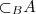
eu achei {-2,-1,1,4,6}
A minha dúvida é: no conj. C entram números como -2, -4,-6? porque no gabarito a resposta dessa questão é {-2,-1,1}
-
Juliane
- Usuário Ativo

-
- Mensagens: 12
- Registrado em: Sáb Set 04, 2010 17:29
- Formação Escolar: ENSINO MÉDIO PROFISSIONALIZANTE
- Área/Curso: Edificações
- Andamento: cursando
 por Juliane » Dom Abr 03, 2011 21:49
por Juliane » Dom Abr 03, 2011 21:49
Eu quis dizer complementar de A em relação a B interseção complementar de C em relação a B
-
Juliane
- Usuário Ativo

-
- Mensagens: 12
- Registrado em: Sáb Set 04, 2010 17:29
- Formação Escolar: ENSINO MÉDIO PROFISSIONALIZANTE
- Área/Curso: Edificações
- Andamento: cursando
Voltar para Álgebra Elementar
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- [Conjuntos] Confusão em teoria dos conjuntos numa questão.
 por Debora Bruna » Seg Jan 11, 2016 17:44
por Debora Bruna » Seg Jan 11, 2016 17:44
- 1 Respostas
- 8842 Exibições
- Última mensagem por DanielFerreira

Sáb Jan 23, 2016 16:44
Conjuntos
-
- [Conjuntos] Dúvida sobre conjuntos vazios
por ALPC » Qui Set 18, 2014 18:28
- 5 Respostas
- 6421 Exibições
- Última mensagem por adauto martins

Seg Set 22, 2014 15:44
Conjuntos
-
- [conjuntos]numeros racionais e conjuntos
por fenixxx » Ter Fev 28, 2012 21:35
- 3 Respostas
- 4730 Exibições
- Última mensagem por DanielFerreira

Sex Mar 02, 2012 00:04
Álgebra Elementar
-
- [Conjuntos] Problema de conjuntos com porcentagem
por Tibes » Qui Jan 31, 2013 14:29
- 1 Respostas
- 7959 Exibições
- Última mensagem por young_jedi

Sex Fev 01, 2013 12:39
Conjuntos
-
- [Conjuntos] Conjuntos e geometria plana
por bencz » Dom Mar 03, 2013 12:58
- 3 Respostas
- 11206 Exibições
- Última mensagem por maison_souza

Sex Nov 14, 2014 13:15
Álgebra Elementar
Usuários navegando neste fórum: Nenhum usuário registrado e 0 visitantes
Assunto:
Unesp - 95 Números Complexos
Autor:
Alucard014 - Dom Ago 01, 2010 18:22
(UNESP - 95) Seja L o Afixo de um Número complexo

em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto.
Assunto:
Unesp - 95 Números Complexos
Autor:
MarceloFantini - Qui Ago 05, 2010 17:27
Seja

o ângulo entre o eixo horizontal e o afixo

. O triângulo é retângulo com catetos

e

, tal que

. Seja

o ângulo complementar. Então

. Como

, o ângulo que o afixo

formará com a horizontal será

, mas negativo pois tem de ser no quarto quadrante. Se

, então

. Como módulo é um:

.
Logo, o afixo é

.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
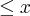 <6}, B={x
<6}, B={x  Z* | -2,6<x
Z* | -2,6<x  13/2 }, C={x | x é um numero inteiro, par, não nulo, e menor que 8}
13/2 }, C={x | x é um numero inteiro, par, não nulo, e menor que 8} = ?
= ?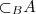 eu achei {-2,-1,1,4,6}
eu achei {-2,-1,1,4,6}
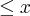 <6}, B={x
<6}, B={x  Z* | -2,6<x
Z* | -2,6<x  13/2 }, C={x | x é um numero inteiro, par, não nulo, e menor que 8}
13/2 }, C={x | x é um numero inteiro, par, não nulo, e menor que 8} = ?
= ?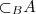 eu achei {-2,-1,1,4,6}
eu achei {-2,-1,1,4,6}


 em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto.
em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto. o ângulo entre o eixo horizontal e o afixo
o ângulo entre o eixo horizontal e o afixo  . O triângulo é retângulo com catetos
. O triângulo é retângulo com catetos  e
e  , tal que
, tal que  . Seja
. Seja  o ângulo complementar. Então
o ângulo complementar. Então  . Como
. Como  , o ângulo que o afixo
, o ângulo que o afixo  formará com a horizontal será
formará com a horizontal será  , mas negativo pois tem de ser no quarto quadrante. Se
, mas negativo pois tem de ser no quarto quadrante. Se  , então
, então  . Como módulo é um:
. Como módulo é um:  .
. .
.