 por gerson25 » Dom Abr 03, 2011 21:25
por gerson25 » Dom Abr 03, 2011 21:25
Estou com duvida nessas questões tentei varias vezes, e não conseguir !!!
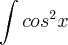
Nessa pensei em separa
u= cosx ; du= -senx
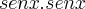

Mais não conferiu na reposta, vi na resolução do livro que ele começou da seguinte forma
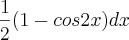
como ele consegui esse
2x??
e na outra questão, eu acredito q precisa-se de primeira que mostrei
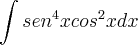
Por favor me mostre como fazer as duas integrais e mostrando pra mim se tem alguma regra, desde ja eu agradeço
-
gerson25
- Novo Usuário

-
- Mensagens: 7
- Registrado em: Qua Fev 23, 2011 22:28
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Mecatrônica
- Andamento: cursando
 por Elcioschin » Dom Abr 03, 2011 21:42
por Elcioschin » Dom Abr 03, 2011 21:42
Sua dúvida é do Enssino Médio:
cos(2x) = cos(x + x)
cos(2x) = cos²x - sen²x
cos(2x) = cos²x - (1 - cos²x)
cos(2x) = 2*cos²x - 1
1 + cos(2x) = 2*cos²x
cos²x = [1 + cos(2x)]/2
Agora é contigo
-
Elcioschin
- Colaborador Voluntário

-
- Mensagens: 624
- Registrado em: Sáb Ago 01, 2009 10:49
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia
- Andamento: formado
 por gerson25 » Dom Abr 03, 2011 23:43
por gerson25 » Dom Abr 03, 2011 23:43
valeu por reposnde, eu tinha pesquisado aqui e achei uma tabela de indentidade trigonometrica.
to sofrendo com essa parte trigonometrica, mais com algumas dificuldades to resovendo os exercicios.
valeu, obrigado.
-
gerson25
- Novo Usuário

-
- Mensagens: 7
- Registrado em: Qua Fev 23, 2011 22:28
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Mecatrônica
- Andamento: cursando
Voltar para Cálculo: Limites, Derivadas e Integrais
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- [integrais] Calculando áreas - Integrais
 por Faby » Seg Set 19, 2011 10:55
por Faby » Seg Set 19, 2011 10:55
- 11 Respostas
- 8811 Exibições
- Última mensagem por LuizAquino

Qua Set 21, 2011 18:03
Cálculo: Limites, Derivadas e Integrais
-
- Integrais
por pseytow » Qui Nov 27, 2008 21:54
- 1 Respostas
- 2804 Exibições
- Última mensagem por Adriano Tavares

Qui Mar 10, 2011 01:52
Cálculo: Limites, Derivadas e Integrais
-
- Integrais
por panneitz » Dom Jun 07, 2009 19:55
- 1 Respostas
- 2436 Exibições
- Última mensagem por Marcampucio

Dom Jun 07, 2009 20:31
Cálculo: Limites, Derivadas e Integrais
-
- Integrais
por leha » Ter Nov 10, 2009 16:08
- 2 Respostas
- 2518 Exibições
- Última mensagem por leha

Sex Nov 13, 2009 08:56
Cálculo: Limites, Derivadas e Integrais
-
- Integrais em IR3
por Saruman » Sáb Mai 22, 2010 10:27
- 1 Respostas
- 2132 Exibições
- Última mensagem por luispereira

Ter Dez 28, 2010 01:45
Cálculo: Limites, Derivadas e Integrais
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
Exercicios de polinomios
Autor:
shaft - Qua Jun 30, 2010 17:30

Então, o exercicio pede para encontrar

.
Bom, tentei resolver a questão acima desenvolvendo as duas partes em ( )...Logo dps cheguei em um resultado q nao soube o q fazer mais.
Se vcs puderem ajudar !
Assunto:
Exercicios de polinomios
Autor:
Douglasm - Qua Jun 30, 2010 17:53
Bom, se desenvolvermos isso, encontramos:

Para que os polinômios sejam iguais, seus respectivos coeficientes devem ser iguais (ax = bx ; ax² = bx², etc.):


Somando a primeira e a segunda equação:

Finalmente:

Até a próxima.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
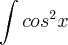
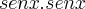

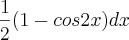
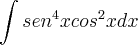




 .
.



