 por Andersonborges » Dom Abr 03, 2011 20:13
por Andersonborges » Dom Abr 03, 2011 20:13
pessoal.. nao consigo sai desse exercio
calcule os limtes
17.
![\lim_{h\rightarrow-4} \frac{\sqrt[]{2({h}^{2}- 8 )}+h}{h+4} \lim_{h\rightarrow-4} \frac{\sqrt[]{2({h}^{2}- 8 )}+h}{h+4}](/latexrender/pictures/18e74d0f0dde44f3065fe0f9657f072f.png)
-
Andersonborges
- Usuário Ativo

-
- Mensagens: 12
- Registrado em: Qui Fev 24, 2011 02:36
- Formação Escolar: ENSINO MÉDIO
- Área/Curso: engenharia eletrica
- Andamento: cursando
 por Andersonborges » Dom Abr 03, 2011 20:14
por Andersonborges » Dom Abr 03, 2011 20:14
folha dde resposta aqui diz ser -1
-
Andersonborges
- Usuário Ativo

-
- Mensagens: 12
- Registrado em: Qui Fev 24, 2011 02:36
- Formação Escolar: ENSINO MÉDIO
- Área/Curso: engenharia eletrica
- Andamento: cursando
 por Elcioschin » Dom Abr 03, 2011 21:36
por Elcioschin » Dom Abr 03, 2011 21:36
Fazendo por L'Hopital
Numerador ----> f(h) = V2*(h²- 8)^(1/2) + h ----> f '(h) = V2*(1/2)*[(h² - 8)^(-1/2)]*h + 1 ----> f '(h) = V2*h/V(h² - 8) + 1
Denomnador ----> g(h) = h ----> g'(h)= 1
Limite {V[2(h² - 8)] + h}/h = Limite [V2*h/V(h² - 8) + 1] = V2*(-4)/V[(-4)² - 8] + 1 = - 4*V2/V8 + 1 = - 2 + 1 = - 1
h--->-4 .........................h--->-4
-
Elcioschin
- Colaborador Voluntário

-
- Mensagens: 624
- Registrado em: Sáb Ago 01, 2009 10:49
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia
- Andamento: formado
 por Andersonborges » Dom Abr 03, 2011 22:04
por Andersonborges » Dom Abr 03, 2011 22:04
amigo.. me tira uma duvida.. esse metodo de l'hopital é unico jeito
eu nao lembro de ter aprendido por esse metodo.
essa materia começo agora... e perdi um dia de aula =(.. vou imprimi sua resposta e interpreta-la
obrigado
-
Andersonborges
- Usuário Ativo

-
- Mensagens: 12
- Registrado em: Qui Fev 24, 2011 02:36
- Formação Escolar: ENSINO MÉDIO
- Área/Curso: engenharia eletrica
- Andamento: cursando
 por LuizAquino » Seg Abr 04, 2011 12:13
por LuizAquino » Seg Abr 04, 2011 12:13
A Regra de L'Hopital é usada para calcular alguns limites quando já se foi estudado o conceito de derivada.
Obviamente, no início do curso de Cálculo vemos apenas limites. Portanto, nesse caso não podemos usar derivadas.
Para resolver o limite que você deseja, multiplique o numerador e denominador por

e use o produto notável
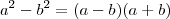
:
![\lim_{h\rightarrow -4} \frac{\sqrt{2({h}^{2}- 8 )}+h}{h+4} = \lim_{h\rightarrow -4} \frac{[\sqrt{2({h}^{2}- 8 )}+h][\sqrt{2({h}^{2}- 8 )}-h]}{(h+4)[\sqrt{2({h}^{2}- 8 )}-h]} \lim_{h\rightarrow -4} \frac{\sqrt{2({h}^{2}- 8 )}+h}{h+4} = \lim_{h\rightarrow -4} \frac{[\sqrt{2({h}^{2}- 8 )}+h][\sqrt{2({h}^{2}- 8 )}-h]}{(h+4)[\sqrt{2({h}^{2}- 8 )}-h]}](/latexrender/pictures/d2f23ce3ec77e0f430c4c6733d2bcfaa.png)
![= \lim_{h\rightarrow -4} \frac{2(h^2-8) - h^2}{(h+4)[\sqrt{2({h}^{2}- 8 )}-h]} = \lim_{h\rightarrow -4} \frac{2(h^2-8) - h^2}{(h+4)[\sqrt{2({h}^{2}- 8 )}-h]}](/latexrender/pictures/d0228e19c7395fecda8e95f19a2fd280.png)
![= \lim_{h\rightarrow -4} \frac{h^2-16}{(h+4)[\sqrt{2({h}^{2}- 8 )}-h]} = \lim_{h\rightarrow -4} \frac{h^2-16}{(h+4)[\sqrt{2({h}^{2}- 8 )}-h]}](/latexrender/pictures/e137c8da3a1ddf09423b1ea54df03391.png)
![= \lim_{h\rightarrow -4} \frac{(h-4)(h+4)}{(h+4)[\sqrt{2({h}^{2}- 8 )}-h]} = \lim_{h\rightarrow -4} \frac{(h-4)(h+4)}{(h+4)[\sqrt{2({h}^{2}- 8 )}-h]}](/latexrender/pictures/41e1b6535b9c4a04613901ff999b24d1.png)
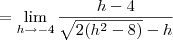
![= \frac{-4-4}{\sqrt{2[(-4)^{2}- 8 ]}-(-4)} = \frac{-4-4}{\sqrt{2[(-4)^{2}- 8 ]}-(-4)}](/latexrender/pictures/5eca0e17c6d451cfad896887f471e794.png)
= -1
SugestãoEu acho que o tópico abaixo pode lhe interessar:
Curso de Cálculo I no YouTubeviewtopic.php?f=137&t=4280
-

LuizAquino
- Colaborador Moderador - Professor

-
- Mensagens: 2654
- Registrado em: Sex Jan 21, 2011 09:11
- Localização: Teófilo Otoni - MG
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Mestrado - Modelagem Computacional
- Andamento: formado
-
 por mindy » Qui Abr 14, 2011 19:47
por mindy » Qui Abr 14, 2011 19:47
Gostaria de tirar uma dúvida,por favor.Como fazer o estudo do limite de Forma Analítica e Geométrica da função(ax+b).Não tentei primeiramente,porque não sei por onde começar.Pois não entendi o enunciado.Se puderem me ajudar.Ficarei imensamente grata.
-
mindy
- Novo Usuário

-
- Mensagens: 3
- Registrado em: Qua Abr 06, 2011 14:21
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Matemática
- Andamento: cursando
 por LuizAquino » Qui Abr 14, 2011 22:31
por LuizAquino » Qui Abr 14, 2011 22:31
Olá mindy,
Por questão de organização, não use tópicos existentes para postar novos exercícios.
Por favor, crie um novo tópico para o seu exercício.
-

LuizAquino
- Colaborador Moderador - Professor

-
- Mensagens: 2654
- Registrado em: Sex Jan 21, 2011 09:11
- Localização: Teófilo Otoni - MG
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Mestrado - Modelagem Computacional
- Andamento: formado
-
Voltar para Cálculo: Limites, Derivadas e Integrais
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- [Cálculo: Limites, Derivadas e Integrais] Cálculo de limites
por jeferson lopes » Ter Mar 26, 2013 08:49
- 2 Respostas
- 5551 Exibições
- Última mensagem por jeferson lopes

Ter Mar 26, 2013 11:52
Cálculo: Limites, Derivadas e Integrais
-
- [limites] exercicio de calculo envolvendo limites
por lucasdemirand » Qua Jul 10, 2013 00:45
- 1 Respostas
- 4798 Exibições
- Última mensagem por e8group

Sáb Jul 20, 2013 13:08
Cálculo: Limites, Derivadas e Integrais
-
- [Limites] Dúvida sobre limites laterais
por Subnik » Sáb Abr 04, 2015 18:24
- 1 Respostas
- 2782 Exibições
- Última mensagem por DanielFerreira

Dom Abr 12, 2015 16:10
Cálculo: Limites, Derivadas e Integrais
-
- [LIMITES] Dúvida em questão de Limites no infinito
 por Jacques » Ter Jul 12, 2016 21:42
por Jacques » Ter Jul 12, 2016 21:42
- 4 Respostas
- 7534 Exibições
- Última mensagem por vitor_jo

Qua Jul 13, 2016 16:51
Cálculo: Limites, Derivadas e Integrais
-
- [Cálculo 2 - Limites] Existência de Limites
por Piva » Seg Abr 16, 2012 11:29
- 0 Respostas
- 5439 Exibições
- Última mensagem por Piva

Seg Abr 16, 2012 11:29
Cálculo: Limites, Derivadas e Integrais
Usuários navegando neste fórum: Nenhum usuário registrado e 0 visitantes
Assunto:
função demanda
Autor:
ssousa3 - Dom Abr 03, 2011 20:55
alguém poderia me ajudar nesse exercício aqui Uma loja de CDs adquire cada unidade por R$20,00 e a revende por R$30,00. Nestas condições,
a quantidade mensal que consegue vender é 500 unidades. O proprietário estima que, reduzindo o preço para R$28,00, conseguirá vender 600 unidades por mês.
a) Obtenha a função demanda, supondo ser linear
Eu faço ensino médio mas compro apostilas de concursos para me preparar para mercado de trabalho e estudar sozinho não é fácil. Se alguém puder me ajudar aqui fico grato
Assunto:
função demanda
Autor:
ssousa3 - Seg Abr 04, 2011 14:30
Gente alguém por favor me ensine a calcular a fórmula da função demanda

Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
![\lim_{h\rightarrow-4} \frac{\sqrt[]{2({h}^{2}- 8 )}+h}{h+4} \lim_{h\rightarrow-4} \frac{\sqrt[]{2({h}^{2}- 8 )}+h}{h+4}](/latexrender/pictures/18e74d0f0dde44f3065fe0f9657f072f.png)

![\lim_{h\rightarrow-4} \frac{\sqrt[]{2({h}^{2}- 8 )}+h}{h+4} \lim_{h\rightarrow-4} \frac{\sqrt[]{2({h}^{2}- 8 )}+h}{h+4}](/latexrender/pictures/18e74d0f0dde44f3065fe0f9657f072f.png)




 e use o produto notável
e use o produto notável 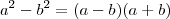 :
:![\lim_{h\rightarrow -4} \frac{\sqrt{2({h}^{2}- 8 )}+h}{h+4} = \lim_{h\rightarrow -4} \frac{[\sqrt{2({h}^{2}- 8 )}+h][\sqrt{2({h}^{2}- 8 )}-h]}{(h+4)[\sqrt{2({h}^{2}- 8 )}-h]} \lim_{h\rightarrow -4} \frac{\sqrt{2({h}^{2}- 8 )}+h}{h+4} = \lim_{h\rightarrow -4} \frac{[\sqrt{2({h}^{2}- 8 )}+h][\sqrt{2({h}^{2}- 8 )}-h]}{(h+4)[\sqrt{2({h}^{2}- 8 )}-h]}](/latexrender/pictures/d2f23ce3ec77e0f430c4c6733d2bcfaa.png)
![= \lim_{h\rightarrow -4} \frac{2(h^2-8) - h^2}{(h+4)[\sqrt{2({h}^{2}- 8 )}-h]} = \lim_{h\rightarrow -4} \frac{2(h^2-8) - h^2}{(h+4)[\sqrt{2({h}^{2}- 8 )}-h]}](/latexrender/pictures/d0228e19c7395fecda8e95f19a2fd280.png)
![= \lim_{h\rightarrow -4} \frac{h^2-16}{(h+4)[\sqrt{2({h}^{2}- 8 )}-h]} = \lim_{h\rightarrow -4} \frac{h^2-16}{(h+4)[\sqrt{2({h}^{2}- 8 )}-h]}](/latexrender/pictures/e137c8da3a1ddf09423b1ea54df03391.png)
![= \lim_{h\rightarrow -4} \frac{(h-4)(h+4)}{(h+4)[\sqrt{2({h}^{2}- 8 )}-h]} = \lim_{h\rightarrow -4} \frac{(h-4)(h+4)}{(h+4)[\sqrt{2({h}^{2}- 8 )}-h]}](/latexrender/pictures/41e1b6535b9c4a04613901ff999b24d1.png)
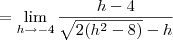
![= \frac{-4-4}{\sqrt{2[(-4)^{2}- 8 ]}-(-4)} = \frac{-4-4}{\sqrt{2[(-4)^{2}- 8 ]}-(-4)}](/latexrender/pictures/5eca0e17c6d451cfad896887f471e794.png)




