 por andersontricordiano » Sáb Abr 02, 2011 04:03
por andersontricordiano » Sáb Abr 02, 2011 04:03
Considere
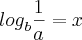
sendo

,
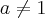
,

e
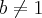
. Expresse
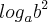
, em termos de x
Detalhe a resposta é:
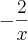
Obrigado quem resolver esse exercício!
-
andersontricordiano
- Colaborador Voluntário

-
- Mensagens: 192
- Registrado em: Sex Mar 04, 2011 23:02
- Formação Escolar: ENSINO MÉDIO
- Andamento: formado
 por Pedro123 » Sáb Abr 02, 2011 12:07
por Pedro123 » Sáb Abr 02, 2011 12:07
se
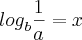
, temos que
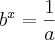
seja

tal que:

, temos então :
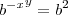
, porém
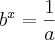

então:
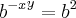
. Desconsiderando as bases...:
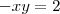
logo
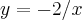
.
abraços qualquer duvida pergunte
Editado pela última vez por
Pedro123 em Sáb Abr 02, 2011 12:08, em um total de 1 vez.
-
Pedro123
- Usuário Parceiro

-
- Mensagens: 60
- Registrado em: Qui Jun 10, 2010 22:46
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Mecanica - 1° Período
- Andamento: cursando
 por FilipeCaceres » Sáb Abr 02, 2011 12:08
por FilipeCaceres » Sáb Abr 02, 2011 12:08
Você só precisa saber fazer mudança de base,
Ex.:
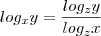
, tendo cuidando com as condições de existencias.
Tende fazer e se não conseguir daí lhe damos mais uma dica.
Abraço.
-
FilipeCaceres
- Colaborador Voluntário

-
- Mensagens: 351
- Registrado em: Dom Out 31, 2010 21:43
- Formação Escolar: ENSINO MÉDIO PROFISSIONALIZANTE
- Área/Curso: Tec. Mecatrônica
- Andamento: formado
Voltar para Logaritmos
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- [Logaritmos] Dúvida em um exercicio envolvendo logaritmos.
por LuizGustavo » Sex Jun 01, 2012 22:48
- 2 Respostas
- 5030 Exibições
- Última mensagem por jefferson0209

Ter Set 22, 2015 18:38
Logaritmos
-
- [Exponencial/Logarítmos] exercício ITA
 por fabiomarine » Ter Ago 28, 2012 16:27
por fabiomarine » Ter Ago 28, 2012 16:27
- 5 Respostas
- 3804 Exibições
- Última mensagem por fabiomarine

Qua Ago 29, 2012 13:23
Logaritmos
-
- [Progressão Aritmética] Exercício P.A + Logaritmos
por jonaspache » Sáb Ago 27, 2011 20:13
- 6 Respostas
- 6156 Exibições
- Última mensagem por jonaspache

Dom Ago 28, 2011 16:06
Progressões
-
- [Logaritmos] equação com logaritmos
por natanaelvoss » Sex Dez 07, 2012 20:25
- 2 Respostas
- 6661 Exibições
- Última mensagem por jefferson0209

Ter Set 22, 2015 18:40
Logaritmos
-
- logaritmos
por celisecorrea » Ter Set 30, 2008 17:17
- 2 Respostas
- 3351 Exibições
- Última mensagem por jefferson0209

Ter Set 22, 2015 18:38
Logaritmos
Usuários navegando neste fórum: Nenhum usuário registrado e 0 visitantes
Assunto:
[calculo] derivada
Autor:
beel - Seg Out 24, 2011 16:59
Para derivar a função
(16-2x)(21-x).x
como é melhor fazer?
derivar primeiro sei la, ((16-2x)(21-x))' achar o resultado (y)
e depois achar (y.x)' ?
Assunto:
[calculo] derivada
Autor:
MarceloFantini - Seg Out 24, 2011 17:15
Você poderia fazer a distributiva e derivar como um polinômio comum.
Assunto:
[calculo] derivada
Autor:
wellersonobelix - Dom Mai 31, 2015 17:26
Funciona da mesma forma que derivada de x.y.z, ou seja, x'.y.z+x.y'.z+x.y.z' substitui cada expressão pelas variáveis e x',y' e z' é derivada de cada um
Assunto:
[calculo] derivada
Autor:
wellersonobelix - Dom Mai 31, 2015 17:31
derivada de (16-2x)=-2
derivada de (21-x)=-1
derivada de x=1
derivada de (16-2x)(21-x)x=-2.(21-x)x+(-1).(16-2x)x +1.(16-2x)(21-x)
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
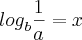 sendo
sendo  ,
,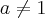 ,
,  e
e 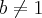 . Expresse
. Expresse 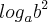 , em termos de x
, em termos de x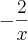

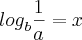 sendo
sendo  ,
,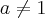 ,
,  e
e 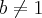 . Expresse
. Expresse 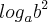 , em termos de x
, em termos de x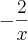

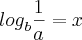 , temos que
, temos que 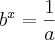
 tal que:
tal que: , temos então :
, temos então :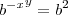 , porém
, porém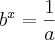

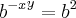 . Desconsiderando as bases...:
. Desconsiderando as bases...: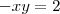 logo
logo 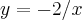 .
.
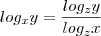 , tendo cuidando com as condições de existencias.
, tendo cuidando com as condições de existencias.