 por Abelardo » Sex Abr 01, 2011 01:06
por Abelardo » Sex Abr 01, 2011 01:06
Estou estudando uma apostila sobre somatório e quando estava olhando as demonstrações das propriedades operatórias da soma (subtração) mas para todas as outras o livro propôs que fizéssemos o restante.
Tentei demonstrar, mas peço que apontem os ''erros'' cometidos, como já espero que hajam vários kkkk.
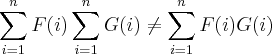
Sei que:
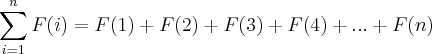
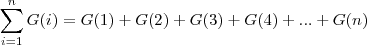
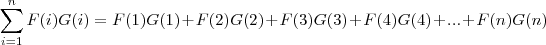
Chamei
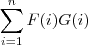
de

Apliquei a distributiva em
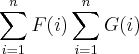
e obtive a igualdade
![F(1)[G(1)+G(2)+G(3)+...+G(n)]+F(2)[G(1)+G(2)+G(3)+...+G(n)]+...+F(n)[G(1)+G(2)+G(3)+...+G(n)] F(1)[G(1)+G(2)+G(3)+...+G(n)]+F(2)[G(1)+G(2)+G(3)+...+G(n)]+...+F(n)[G(1)+G(2)+G(3)+...+G(n)]](/latexrender/pictures/65e86a1300a78c56f92826c25a7cda28.png)
.
Percebi que

está contido em
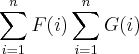
.
![\sum_{i=1}^{n}F(i)\sum_{i=1}^{n}G(i)=\Omega + F(1)[G(2)+G(3)+G(4)+...+G(n)]+F(2)[G(1)+G(3)+G(4)+...+G(n)]+...+F(n)[G(1)+G(2)+G(3)+...+G(n-1)] \sum_{i=1}^{n}F(i)\sum_{i=1}^{n}G(i)=\Omega + F(1)[G(2)+G(3)+G(4)+...+G(n)]+F(2)[G(1)+G(3)+G(4)+...+G(n)]+...+F(n)[G(1)+G(2)+G(3)+...+G(n-1)]](/latexrender/pictures/25f44fb30d0faf99d80ed98454760063.png)
Então posso concluir que
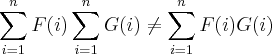
?
-

Abelardo
- Colaborador Voluntário

-
- Mensagens: 159
- Registrado em: Qui Mar 03, 2011 01:45
- Formação Escolar: ENSINO MÉDIO
- Andamento: cursando
Voltar para Álgebra Elementar
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Somatório
por ARCS » Sáb Mar 12, 2011 01:51
- 3 Respostas
- 4090 Exibições
- Última mensagem por Renato_RJ

Sáb Mar 12, 2011 03:14
Sequências
-
- Somatório
por alienante » Qua Mai 07, 2014 14:59
- 1 Respostas
- 1432 Exibições
- Última mensagem por Russman

Qua Mai 07, 2014 19:14
Álgebra Elementar
-
- Somatório e Produtório
por Abelardo » Qua Mar 23, 2011 13:49
- 1 Respostas
- 6350 Exibições
- Última mensagem por Neperiano

Dom Ago 07, 2011 22:12
Pedidos de Materiais
-
- Somatório de fatoriais
por Prof Prevaricador » Dom Abr 14, 2013 22:28
- 1 Respostas
- 2341 Exibições
- Última mensagem por marciosouza

Qua Abr 17, 2013 23:21
Sequências
-
- Somatório - limite
por livia02 » Sex Ago 16, 2013 16:31
- 1 Respostas
- 3452 Exibições
- Última mensagem por young_jedi

Sex Ago 16, 2013 19:12
Cálculo: Limites, Derivadas e Integrais
Usuários navegando neste fórum: Nenhum usuário registrado e 0 visitantes
Assunto:
cálculo de limites
Autor:
Hansegon - Seg Ago 25, 2008 11:29
Bom dia.
Preciso de ajuda na solução deste problema, pois só chego ao resultado de 0 sobre 0.
Obrigado
\lim_{x\rightarrow-1} x³ +1/x²-1[/tex]
Assunto:
cálculo de limites
Autor:
Molina - Seg Ago 25, 2008 13:25

Realmente se você jogar o -1 na equação dá 0 sobre 0.
Indeterminações deste tipo você pode resolver por L'Hôpital
que utiliza derivada.
Outro modo é transformar o numerador e/ou denominador
para que não continue dando indeterminado.
Dica: dividir o numerador e o denominador por algum valor é uma forma que normalmente dá certo.

Caso ainda não tenha dado uma

, avisa que eu resolvo.
Bom estudo!
Assunto:
cálculo de limites
Autor:
Guill - Dom Abr 08, 2012 16:03



Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
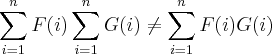
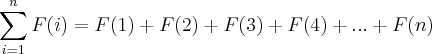
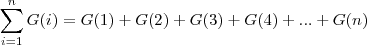
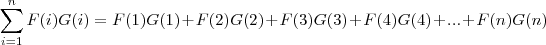
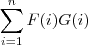 de
de 
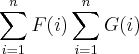 e obtive a igualdade
e obtive a igualdade![F(1)[G(1)+G(2)+G(3)+...+G(n)]+F(2)[G(1)+G(2)+G(3)+...+G(n)]+...+F(n)[G(1)+G(2)+G(3)+...+G(n)] F(1)[G(1)+G(2)+G(3)+...+G(n)]+F(2)[G(1)+G(2)+G(3)+...+G(n)]+...+F(n)[G(1)+G(2)+G(3)+...+G(n)]](/latexrender/pictures/65e86a1300a78c56f92826c25a7cda28.png) .
.  está contido em
está contido em 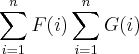 .
.![\sum_{i=1}^{n}F(i)\sum_{i=1}^{n}G(i)=\Omega + F(1)[G(2)+G(3)+G(4)+...+G(n)]+F(2)[G(1)+G(3)+G(4)+...+G(n)]+...+F(n)[G(1)+G(2)+G(3)+...+G(n-1)] \sum_{i=1}^{n}F(i)\sum_{i=1}^{n}G(i)=\Omega + F(1)[G(2)+G(3)+G(4)+...+G(n)]+F(2)[G(1)+G(3)+G(4)+...+G(n)]+...+F(n)[G(1)+G(2)+G(3)+...+G(n-1)]](/latexrender/pictures/25f44fb30d0faf99d80ed98454760063.png)
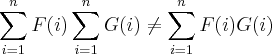 ?
?
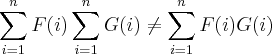
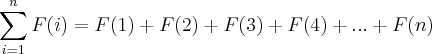
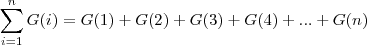
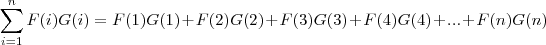
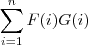 de
de 
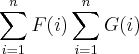 e obtive a igualdade
e obtive a igualdade![F(1)[G(1)+G(2)+G(3)+...+G(n)]+F(2)[G(1)+G(2)+G(3)+...+G(n)]+...+F(n)[G(1)+G(2)+G(3)+...+G(n)] F(1)[G(1)+G(2)+G(3)+...+G(n)]+F(2)[G(1)+G(2)+G(3)+...+G(n)]+...+F(n)[G(1)+G(2)+G(3)+...+G(n)]](/latexrender/pictures/65e86a1300a78c56f92826c25a7cda28.png) .
.  está contido em
está contido em 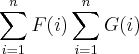 .
.![\sum_{i=1}^{n}F(i)\sum_{i=1}^{n}G(i)=\Omega + F(1)[G(2)+G(3)+G(4)+...+G(n)]+F(2)[G(1)+G(3)+G(4)+...+G(n)]+...+F(n)[G(1)+G(2)+G(3)+...+G(n-1)] \sum_{i=1}^{n}F(i)\sum_{i=1}^{n}G(i)=\Omega + F(1)[G(2)+G(3)+G(4)+...+G(n)]+F(2)[G(1)+G(3)+G(4)+...+G(n)]+...+F(n)[G(1)+G(2)+G(3)+...+G(n-1)]](/latexrender/pictures/25f44fb30d0faf99d80ed98454760063.png)
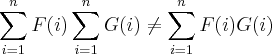 ?
?


 , avisa que eu resolvo.
, avisa que eu resolvo.

