 por Elcioschin » Qui Mar 31, 2011 12:55
por Elcioschin » Qui Mar 31, 2011 12:55
Não vejo nenhuma função!!!
Calcule a PA ??????
Imagino que seja:
Dada a PA -----> x, 1/2, - 2/3
Calculando x ----> a1 + a3 = 2*a2 ----> x - 2/3 = (2*1/2) ----> x - 2/3 = 1 ----> x = 5/3
No segundo a PA já foi fornecida !!!!!!. Suponho que esteja sendo pedida a razão da PA. Se for, deixo contigo, pois é uma simples aplicação da fórmula. Suponho que vc conheça. Se não, aconselho-a a estudar a teoria.
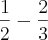 )
)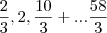

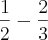 )
)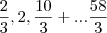


![\frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}} \frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}}](/latexrender/pictures/981987c7bcdf9f8f498ca4605785636a.png)
![\sqrt[]{2} \sqrt[]{2}](/latexrender/pictures/f21662d1cabab6e8b273a4b6f1cd663a.png) (dica : igualar a expressão a
(dica : igualar a expressão a  e elevar ao quadrado os dois lados)
e elevar ao quadrado os dois lados)