 por ronneysantos » Dom Mar 27, 2011 21:05
por ronneysantos » Dom Mar 27, 2011 21:05
Srs,
Sou novo no forum e este é meu primeiro post. Espero poder ajudar e ser ajudado.
Bem, estou com um problema e sei que o resultado é Zero. Entretanto não sei como manupular isso com alguma Lei ou Fórmula que, de tal forma, consiga achar o resultado. Imagino que seja fácil mas nunca ví exercício do tipo.
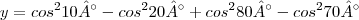
Muito obrigado a todos.
Ronney
-
ronneysantos
- Novo Usuário

-
- Mensagens: 7
- Registrado em: Dom Mar 27, 2011 20:31
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia
- Andamento: cursando
 por Molina » Dom Mar 27, 2011 21:40
por Molina » Dom Mar 27, 2011 21:40
Boa noite, Ronney.
Bem-vindo e obrigado por confiar no site.
Para sua questão, basta usar uma simples relação trigonométrica em dois dos quatro cossenos. A relação é:

Faça esta transformação que você encontrará algum do tipo de

.
Tente fazer e caso não consiga resolver avise que ajudaremos de novo.
Bom estudo

Diego Molina |
CV |
FB |
.COMEquipe AjudaMatemática.com"Existem 10 tipos de pessoas: as que conhecem o sistema binário e as que não conhecem."
-

Molina
- Colaborador Moderador - Professor

-
- Mensagens: 1551
- Registrado em: Dom Jun 01, 2008 14:10
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Licenciatura em Matemática - UFSC
- Andamento: formado
 por ronneysantos » Dom Mar 27, 2011 22:44
por ronneysantos » Dom Mar 27, 2011 22:44
Sr. Molina,
Fico muito grato pela ajuda. Estou ainda mais contente pelo fato de não ter dado a resposta e sim a ferramenta.
Vou tentar aqui e qualquer coisa volto a postar comentarios.
Muito Obrigado.
-
ronneysantos
- Novo Usuário

-
- Mensagens: 7
- Registrado em: Dom Mar 27, 2011 20:31
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia
- Andamento: cursando
 por Molina » Ter Mar 29, 2011 20:52
por Molina » Ter Mar 29, 2011 20:52
ronneysantos escreveu:Sr. Molina,
Fico muito grato pela ajuda. Estou ainda mais contente pelo fato de não ter dado a resposta e sim a ferramenta.
Vou tentar aqui e qualquer coisa volto a postar comentarios.
Muito Obrigado.
E ae, conseguiu?
Diego Molina |
CV |
FB |
.COMEquipe AjudaMatemática.com"Existem 10 tipos de pessoas: as que conhecem o sistema binário e as que não conhecem."
-

Molina
- Colaborador Moderador - Professor

-
- Mensagens: 1551
- Registrado em: Dom Jun 01, 2008 14:10
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Licenciatura em Matemática - UFSC
- Andamento: formado
 por ronneysantos » Qui Mar 31, 2011 09:18
por ronneysantos » Qui Mar 31, 2011 09:18
É Sr. Molina, tô vendo que vc gente boa pra caramba.....
Vamos lá:
Bem, fiz a aplicação da propriedade que vc havia mensionado e ficou assim:

Só que daí como é possível fazer os "cortes" , sendo tal situação? Lembrando que todos na formula vão se cancelar pois o resultado final é Zero.
Obrigado,
Ronney
-
ronneysantos
- Novo Usuário

-
- Mensagens: 7
- Registrado em: Dom Mar 27, 2011 20:31
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia
- Andamento: cursando
 por FilipeCaceres » Qui Mar 31, 2011 10:13
por FilipeCaceres » Qui Mar 31, 2011 10:13
Observe que:

Logo,
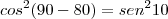
Analogamente temos,

Portanto,

O resto deixo por sua conta.
Espero ter ajudado.
-
FilipeCaceres
- Colaborador Voluntário

-
- Mensagens: 351
- Registrado em: Dom Out 31, 2010 21:43
- Formação Escolar: ENSINO MÉDIO PROFISSIONALIZANTE
- Área/Curso: Tec. Mecatrônica
- Andamento: formado
 por ronneysantos » Qui Mar 31, 2011 10:59
por ronneysantos » Qui Mar 31, 2011 10:59
Agora foi....
Muito Obrigado, consegui resolver.
-
ronneysantos
- Novo Usuário

-
- Mensagens: 7
- Registrado em: Dom Mar 27, 2011 20:31
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia
- Andamento: cursando
Voltar para Trigonometria
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- LEI dos COSSENOS PROBLEMA
 por emarga » Sex Out 26, 2018 16:52
por emarga » Sex Out 26, 2018 16:52
- 2 Respostas
- 3283 Exibições
- Última mensagem por emarga

Qua Nov 07, 2018 17:49
Trigonometria
-
- Problema Elementar de Sin, Cos e Tan
por ronneysantos » Qui Mar 31, 2011 11:31
- 3 Respostas
- 2901 Exibições
- Última mensagem por ronneysantos

Qui Mar 31, 2011 14:08
Trigonometria
-
- [Algebra Elementar] Dúvida em resposta do problema
por marco70 » Ter Jun 14, 2016 14:52
- 0 Respostas
- 1837 Exibições
- Última mensagem por marco70

Ter Jun 14, 2016 14:52
Álgebra Elementar
-
- Lei dos Cossenos
por Joseaugusto » Ter Mar 06, 2012 11:43
- 4 Respostas
- 2994 Exibições
- Última mensagem por Joseaugusto

Ter Mar 06, 2012 22:42
Trigonometria
-
- Lei dos cossenos
por kandara » Qua Abr 30, 2014 17:35
- 1 Respostas
- 4569 Exibições
- Última mensagem por Russman

Qua Abr 30, 2014 18:54
Trigonometria
Usuários navegando neste fórum: Nenhum usuário registrado e 0 visitantes
Assunto:
Unesp - 95 Números Complexos
Autor:
Alucard014 - Dom Ago 01, 2010 18:22
(UNESP - 95) Seja L o Afixo de um Número complexo

em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto.
Assunto:
Unesp - 95 Números Complexos
Autor:
MarceloFantini - Qui Ago 05, 2010 17:27
Seja

o ângulo entre o eixo horizontal e o afixo

. O triângulo é retângulo com catetos

e

, tal que

. Seja

o ângulo complementar. Então

. Como

, o ângulo que o afixo

formará com a horizontal será

, mas negativo pois tem de ser no quarto quadrante. Se

, então

. Como módulo é um:

.
Logo, o afixo é

.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
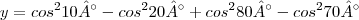



 .
.



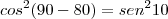



 em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto.
em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto. o ângulo entre o eixo horizontal e o afixo
o ângulo entre o eixo horizontal e o afixo  . O triângulo é retângulo com catetos
. O triângulo é retângulo com catetos  e
e  , tal que
, tal que  . Seja
. Seja  o ângulo complementar. Então
o ângulo complementar. Então  . Como
. Como  , o ângulo que o afixo
, o ângulo que o afixo  formará com a horizontal será
formará com a horizontal será  , então
, então  . Como módulo é um:
. Como módulo é um:  .
. .
.