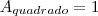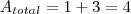por andersontricordiano » Qua Mar 16, 2011 16:43
por andersontricordiano » Qua Mar 16, 2011 16:43
(U F MG) Na figura
ABC é um triângulo retângulo com catetos de medidas
BC=3 e
BA=4; a circunferência de centro
O, inscrita no triângulo, tangencia-o nos pontos
D e
E. Determine a área do poligono
ABEODResposta: 4

- triangulo e circulo.jpg (10.5 KiB) Exibido 5250 vezes
Por favor me ajudem a resolver esse calculo!
Obrigado quem me ajudar!!!!
Editado pela última vez por
andersontricordiano em Qua Mar 16, 2011 19:23, em um total de 1 vez.
-
andersontricordiano
- Colaborador Voluntário

-
- Mensagens: 192
- Registrado em: Sex Mar 04, 2011 23:02
- Formação Escolar: ENSINO MÉDIO
- Andamento: formado
 por LuizAquino » Qua Mar 16, 2011 17:41
por LuizAquino » Qua Mar 16, 2011 17:41
Analise a figura abaixo e responda as perguntas.

- triangulo-exercicio-ufmg.png (7.15 KiB) Exibido 5238 vezes
1) Qual a relação que existe entre os triângulos AGO e ADO? E entre os triângulos OEC e ODC?
2) Qual é a medida de AG? E de EC?
-

LuizAquino
- Colaborador Moderador - Professor

-
- Mensagens: 2654
- Registrado em: Sex Jan 21, 2011 09:11
- Localização: Teófilo Otoni - MG
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Mestrado - Modelagem Computacional
- Andamento: formado
-
 por LucasVNPKBS » Sex Mar 25, 2011 16:12
por LucasVNPKBS » Sex Mar 25, 2011 16:12
Ae você so precisa usar a relação:
Raio= Semiperimetro do triangulo - Lado maior do triagulo
Você vai achar o raio igual a 1, e pronto, na hora de calcular a área fica muito fácil, calcula uma de cada vez, soma tudo e o resultado da igual a 4.
-
LucasVNPKBS
- Novo Usuário

-
- Mensagens: 1
- Registrado em: Ter Mar 22, 2011 16:03
- Formação Escolar: ENSINO MÉDIO
- Área/Curso: Pré-Vestibulando
- Andamento: formado
 por MarceloFantini » Sex Mar 25, 2011 16:46
por MarceloFantini » Sex Mar 25, 2011 16:46
Recomendaria que você não usasse o resultado que o Lucas mencionou por razões de que isso acaba tornando-se decoreba e se você não sabe resolver sem gerará problemas futuramente.
Futuro MATEMÁTICO
-
MarceloFantini
- Colaborador Moderador

-
- Mensagens: 3126
- Registrado em: Seg Dez 14, 2009 11:41
- Formação Escolar: GRADUAÇÃO
- Andamento: formado
 por profmatematica » Sex Mar 25, 2011 19:16
por profmatematica » Sex Mar 25, 2011 19:16
Pois eu seguiria a ideia do Lucas sim pode fazer q sai beleza o exercicio
-
profmatematica
- Usuário Dedicado

-
- Mensagens: 42
- Registrado em: Sex Ago 27, 2010 13:34
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: licenciatura em matemática
- Andamento: formado
 por MarceloFantini » Sex Mar 25, 2011 19:51
por MarceloFantini » Sex Mar 25, 2011 19:51
Não adiantar sair se não entender porque saiu.
Futuro MATEMÁTICO
-
MarceloFantini
- Colaborador Moderador

-
- Mensagens: 3126
- Registrado em: Seg Dez 14, 2009 11:41
- Formação Escolar: GRADUAÇÃO
- Andamento: formado
 por FilipeCaceres » Sex Mar 25, 2011 23:48
por FilipeCaceres » Sex Mar 25, 2011 23:48
-
FilipeCaceres
- Colaborador Voluntário

-
- Mensagens: 351
- Registrado em: Dom Out 31, 2010 21:43
- Formação Escolar: ENSINO MÉDIO PROFISSIONALIZANTE
- Área/Curso: Tec. Mecatrônica
- Andamento: formado
 por profmatematica » Sáb Mar 26, 2011 00:39
por profmatematica » Sáb Mar 26, 2011 00:39
Felipe parabens ficou clara logica e precisa sua explicacao
-
profmatematica
- Usuário Dedicado

-
- Mensagens: 42
- Registrado em: Sex Ago 27, 2010 13:34
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: licenciatura em matemática
- Andamento: formado
 por LuizAquino » Sáb Mar 26, 2011 10:21
por LuizAquino » Sáb Mar 26, 2011 10:21
Vejamos como solucionar o exercício usando o caminho que eu havia indicado inicialmente. Nós usaremos
Congruência de Triângulos.
1) Qual a relação que existe entre os triângulos AGO e ADO? E entre os triângulos OEC e ODC?
Temos os triângulos retângulos AGO e ADO. Eles possuem a mesma hipotenusa (AO) e um mesmo cateto (GO=OD=r). Portanto, AG=AD. Desse modo, AGO e ADO são congruentes pelo caso LLL.
De modo análogo, OEC e ODC também são congruentes pelo caso LLL.
2) Qual é a medida de AG? E de EC?
Como ilustrou
filipecaceres, temos que AG=4-r e EC=3-r.
Agora, após respondido as duas peguntas que eu havia feito, bastava pensar um pouquinho e chegar a conclusão que (4-r)+(3-r)=AC.
Lembrando que ABC é um triângulo retângulo, que AC é a hipotenusa e os catetos são AB=4 e BC=3, teremos que AC=5. A partir daí basta montar a equação (4-r)+(3-r)=5 e continuar a solução como indicou
filipecaceres.
-

LuizAquino
- Colaborador Moderador - Professor

-
- Mensagens: 2654
- Registrado em: Sex Jan 21, 2011 09:11
- Localização: Teófilo Otoni - MG
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Mestrado - Modelagem Computacional
- Andamento: formado
-
Voltar para Geometria Plana
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Geometria Analítica - Polígono regular
por fyensinomedio » Sex Nov 08, 2013 13:04
- 1 Respostas
- 2828 Exibições
- Última mensagem por e8group

Sex Nov 08, 2013 20:38
Geometria Analítica
-
- [GEOMETRIA] Calcular o lado de um polígono
por milenaponte » Qui Jun 11, 2015 12:15
- 2 Respostas
- 3124 Exibições
- Última mensagem por milenaponte

Qui Jun 11, 2015 21:39
Geometria Plana
-
- [Geometria Plana] Polígono Regular
por edinaldoprof » Seg Fev 13, 2017 14:08
- 0 Respostas
- 2395 Exibições
- Última mensagem por edinaldoprof

Seg Fev 13, 2017 14:08
Geometria Plana
-
- Determine a área total e o volume do prisma Hexagonal
por andersontricordiano » Qui Nov 10, 2011 15:55
- 1 Respostas
- 3413 Exibições
- Última mensagem por MarceloFantini

Qui Nov 10, 2011 19:54
Geometria
-
- [Geometria Plana] Determine X e Y
por luiz Carlos da Silva » Sex Mar 28, 2014 23:28
- 0 Respostas
- 921 Exibições
- Última mensagem por luiz Carlos da Silva

Sex Mar 28, 2014 23:28
Geometria Plana
Usuários navegando neste fórum: Nenhum usuário registrado e 2 visitantes
Assunto:
Funções
Autor:
Emilia - Sex Dez 03, 2010 13:24
Preciso de ajuda no seguinte problema:
O governo de um Estado Brasileiro mudou a contribuição previdenciária de seus contribuintes. era de 6% sobre qualquer salário; passou para 11% sobre o que excede R$1.200,00 nos salários. Por exemplo, sobre uma salário de R$1.700,00, a contribuição anterior era: 0,06x R$1.700,00 = R$102,00; e a atual é: 0,11x(R$1.700,00 - R$1.200,00) = R$55,00.
i. Determine as funções que fornecem o valor das contribuições em função do valor x do salário antes e depois da mudança na forma de cobrança.
ii. Esboce seus gráficos.
iii. Determine os valores de salários para os quais:
- a contribuição diminuiu;
- a contribuição permaneceu a mesma;
- a contribuição aumentou.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.