Verificar se existem números reais x tais que...

por **Aliocha Karamazov** » Sex Mar 25, 2011 15:39

Olá, pessoal, estou tentanto fazer esse exercício, chego a uma resposta que sei estar errada, mas não consigo encontrar onde estou errando.
O exercício é o seguite:

Verificar se existem números reais x tais que $2-x=\sqrt {x^2 -12}$

Olhem como eu tentei fazer:

$(2-x)^2=(\sqrt{x^2-12})^2\Rightarrow4-4x+x^2=x^2-12\Rightarrow4x=16\Rightarrow x=4$

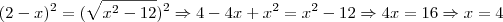
Mas, quando x é substituído por 4, o resultado está errado. De fato, no livro a resposta é $\nexists x \in\mathds$

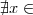
Gostaria de uma ajuda para entender o que estou fazendo de errado. Obrigado!

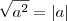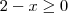
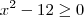
por **LuizAquino** » Sex Mar 25, 2011 15:51

O seu erro está em esquecer da seguinte propriedade:

Se a é um número real qualquer, então $\sqrt{a^2}=|a|$ .

Além disso, lembre-se que a solução deve atender a duas condições:
(i) $2-x\geq 0$
(ii) $x^2-12 \geq 0$