PA - Demonstração

por **jessicaccs** » Sex Mar 25, 2011 11:52

A questão é a seguinte:

Se numa PA a soma dos m primeiros termos é igual à soma dos n primeiros termos, 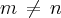$m\,\neq\,n$ , mostre que a soma m+n primeiros termos é igual a zero.

Considerei que m<n e desenvolvi $S{}_{m}\,=\,S{}_{n}$ . Consegui achar a seguinte relação:

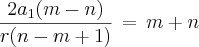$\frac{2a{}_{1}(m-n)}{r(n-m+1)}\,=\,m+n$ (I)

Em seguida desenvolvi $S{}_{m+n}$

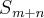
No final de tudo, joguei (I) nessa soma e achei:

$S{}_{m+n}=\,\frac{a{}_{1}(m-n)}{n-m+1}$

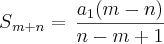
Não deu zero. Não sei se errei em alguma coisa durante a "sopa de letras" que fiz.

Depois tentei achar alguma outra relação.
Pensei o seguinte:
Se m<n, então, tenho que $S{}_{n-m}=S{}_{n}-S{}_{m}$ .
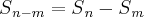Do enunciado eu posso tirar que: $S{}_{n}-S{}_{m}=0$
E, portanto: $S{}_{n-m}=0$

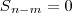
Logo:
$(a{}_{m}+a{}_{n})(n-m)=0$

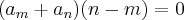
e, $a{}_{m}=-a{}_{n}$

Desenvolvendo-o, consegui achar a seguinte relação:
$m+n=2\left(\frac{a{}_{1}+r}{r} \right)$
Mas, não consegui chegar a nenhum lugar com ela, também.

Obrigada.

por **Elcioschin** » Sex Mar 25, 2011 14:55

Como você não mostrou o desenvolvimento, não dá para saber onde você errou.
Veja a solução completa, considerando a1 = a como 1º termo

am = a + (m - 1)*r -----> Sm = (a + am)*m/2 ----> Sm = (2a + r*m - r)*m/2 ----> Sm = (2a*m + r*m² - r*m)/2

an = a + (n - 1)*r ------> Sn = (a + an)*n/2 ----> Sn = (2a + r*n - r)*n/2 ----> Sn = (2a*n + r*n² - r*n)/2

Igualando ----> (2a*m + r*m² - r*m)/2 = (2a*n + r*n² - r*n)/2 ----> r*m² - r*n² - r*m + r*n + 2a*m - 2a*n = 0

r*(m² - n²) - r*(m - n) + 2a*(m - n) = 0 ----> r*(m + n)*(m - n) - r*(m - n) + 2a*(m - n) = 0 ----> [r*(m + n - 1) - 2a]*(m - n) = 0

Como m <> n podemos dividir por m - n ----> r*(m + n - 1) + 2a = 0 ----> r*(m + n - 1) = - 2a ----> (I)

am+n = a + (m + n - 1)*r -----> Sm+n = [(2a + (m + n - 1)*r]/2 ----> (II)

Substituindo I em II ----> Sm+n = (2a - 2a)*r*n/2 -----> Sm+n = 0

PA - Demonstração

PA - Demonstração

PA - Demonstração

Re: PA - Demonstração

Quem está online