 por andersontricordiano » Qui Mar 24, 2011 16:55
por andersontricordiano » Qui Mar 24, 2011 16:55
Se log 2= a e log 3= b, calcule em função de a e b os seguintes logaritmos decimais:a) log 5
b)
![log\sqrt[5]{72} log\sqrt[5]{72}](/latexrender/pictures/c9dae4e1c71ff3ad2fe4030029f4e543.png)
c)log 500
Resposta:a) 1-a
b)
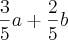
c) 3- a
Eu estou tentando resolver esse três calculo . Mas eu não estou conseguindo!
Obrigado quem resolver esse exercício!
-
andersontricordiano
- Colaborador Voluntário

-
- Mensagens: 192
- Registrado em: Sex Mar 04, 2011 23:02
- Formação Escolar: ENSINO MÉDIO
- Andamento: formado
 por Elcioschin » Qui Mar 24, 2011 19:27
por Elcioschin » Qui Mar 24, 2011 19:27
1) log5 = log(10/2) = log10 - log2 = 1 - a
2) log[72^(1/5)] = (1/5)*log72 = (1/5)*log(2³*3²) = (1/5)*log(2³ + log3²) = (1/5)*(3log2 + 2log3) = 3a/5 + 2b/5
Faça você o terceiro
-
Elcioschin
- Colaborador Voluntário

-
- Mensagens: 624
- Registrado em: Sáb Ago 01, 2009 10:49
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia
- Andamento: formado
 por profmatematica » Sex Mar 25, 2011 12:02
por profmatematica » Sex Mar 25, 2011 12:02
Primeiramente sempre que nao aparece a base tu tens q ter em mente que a base vale 10 certo? Entao log5 vamos pensar 10/2=5 e pela regra o log a/b=a-b ok? Entao log10/2= log10-log2 ok? Log de 10 na base 10=1 e log2 foi dado que vale a entao assim temos log5=log10/2=log10-log2=1 - a entendido?
-
profmatematica
- Usuário Dedicado

-
- Mensagens: 42
- Registrado em: Sex Ago 27, 2010 13:34
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: licenciatura em matemática
- Andamento: formado
 por profmatematica » Sex Mar 25, 2011 12:17
por profmatematica » Sex Mar 25, 2011 12:17
Log500=fatora o 500
temos log500=2ao quadrado.5 elevado ao cubo entao loga.b=loga +logb entao lo500= 2.log2+3log5 entao vem que 2.a+3.(1-a) =3-a espero ter ajudado
-
profmatematica
- Usuário Dedicado

-
- Mensagens: 42
- Registrado em: Sex Ago 27, 2010 13:34
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: licenciatura em matemática
- Andamento: formado
Voltar para Logaritmos
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Calcule em função de a e b os seguintes logaritmos decimais
por andersontricordiano » Qui Mar 24, 2011 16:57
- 1 Respostas
- 1427 Exibições
- Última mensagem por LuizAquino

Qui Mar 24, 2011 17:23
Logaritmos
-
- Calcule em função o logaritmo.
por andersontricordiano » Sáb Abr 02, 2011 17:54
- 1 Respostas
- 1719 Exibições
- Última mensagem por Elcioschin

Sáb Abr 02, 2011 23:27
Logaritmos
-
- logaritmos em função de a e b
por crfsatisfaction » Seg Jul 25, 2011 22:00
- 1 Respostas
- 2367 Exibições
- Última mensagem por Molina

Seg Jul 25, 2011 23:51
Logaritmos
-
- Calcule a função que contem logaritmo
por andersontricordiano » Qui Mai 05, 2011 20:19
- 4 Respostas
- 2155 Exibições
- Última mensagem por andersontricordiano

Sex Mai 06, 2011 16:38
Funções
-
- Calcule a raiz da função do 1º grau?
por breno1323 » Ter Jun 05, 2012 11:44
- 3 Respostas
- 1758 Exibições
- Última mensagem por joaofonseca

Ter Jun 05, 2012 12:30
Funções
Usuários navegando neste fórum: Nenhum usuário registrado e 2 visitantes
Assunto:
Unesp - 95 Números Complexos
Autor:
Alucard014 - Dom Ago 01, 2010 18:22
(UNESP - 95) Seja L o Afixo de um Número complexo

em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto.
Assunto:
Unesp - 95 Números Complexos
Autor:
MarceloFantini - Qui Ago 05, 2010 17:27
Seja

o ângulo entre o eixo horizontal e o afixo

. O triângulo é retângulo com catetos

e

, tal que

. Seja

o ângulo complementar. Então

. Como

, o ângulo que o afixo

formará com a horizontal será

, mas negativo pois tem de ser no quarto quadrante. Se

, então

. Como módulo é um:

.
Logo, o afixo é

.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
![log\sqrt[5]{72} log\sqrt[5]{72}](/latexrender/pictures/c9dae4e1c71ff3ad2fe4030029f4e543.png)
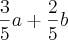

![log\sqrt[5]{72} log\sqrt[5]{72}](/latexrender/pictures/c9dae4e1c71ff3ad2fe4030029f4e543.png)
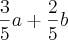






 em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto.
em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto. o ângulo entre o eixo horizontal e o afixo
o ângulo entre o eixo horizontal e o afixo  . O triângulo é retângulo com catetos
. O triângulo é retângulo com catetos  e
e  , tal que
, tal que  . Seja
. Seja  o ângulo complementar. Então
o ângulo complementar. Então  . Como
. Como  , o ângulo que o afixo
, o ângulo que o afixo  formará com a horizontal será
formará com a horizontal será  , mas negativo pois tem de ser no quarto quadrante. Se
, mas negativo pois tem de ser no quarto quadrante. Se  , então
, então  . Como módulo é um:
. Como módulo é um:  .
. .
.