 por renanrdaros » Sex Mar 25, 2011 10:58
por renanrdaros » Sex Mar 25, 2011 10:58
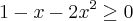
Chego sempre no resultado: S=
![\left(-\infty;-1 \right] \cup \left[\frac{1}{2};+\infty \right) \left(-\infty;-1 \right] \cup \left[\frac{1}{2};+\infty \right)](/latexrender/pictures/c29febe6c056dcd612e61c5a6dbc1b21.png)
Mas o resultado do livro é:
![\left[-1;\frac{1}{2} \right] \left[-1;\frac{1}{2} \right]](/latexrender/pictures/9ff7930624f606598a07c05317984474.png)
Quem tá errado?
-
renanrdaros
- Usuário Parceiro

-
- Mensagens: 54
- Registrado em: Sáb Mar 19, 2011 19:37
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Eng. de Computação
- Andamento: cursando
 por renanrdaros » Sex Mar 25, 2011 11:03
por renanrdaros » Sex Mar 25, 2011 11:03
Se faço pelo método da fatoração e depois dividindo o problema em dois casos, chego no meu resultado.
Se faço pelo método do ma-ca-ma, chego no resultado do livro.
-
renanrdaros
- Usuário Parceiro

-
- Mensagens: 54
- Registrado em: Sáb Mar 19, 2011 19:37
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Eng. de Computação
- Andamento: cursando
 por profmatematica » Sex Mar 25, 2011 11:48
por profmatematica » Sex Mar 25, 2011 11:48
Visto que a=-2 temos uma parabola c concavidade voltada para baixo e se jogarmos no intervalo esta parabola temos o estudo do sinal assim valores negativos a esquerda de -1 e a direita de 1/2 e os valores positivos estarao entre -1e 1/2 certo? Entao volte na equacao e veja que ele pede valores maiores ou iguais a zero entao a resposta e [-1;1/2] entendido amigo?
-
profmatematica
- Usuário Dedicado

-
- Mensagens: 42
- Registrado em: Sex Ago 27, 2010 13:34
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: licenciatura em matemática
- Andamento: formado
 por renanrdaros » Sex Mar 25, 2011 12:10
por renanrdaros » Sex Mar 25, 2011 12:10
-
renanrdaros
- Usuário Parceiro

-
- Mensagens: 54
- Registrado em: Sáb Mar 19, 2011 19:37
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Eng. de Computação
- Andamento: cursando
 por LuizAquino » Sex Mar 25, 2011 15:46
por LuizAquino » Sex Mar 25, 2011 15:46
renanrdaros escreveu:Vou colar aqui a resolução. Quem sabe alguém me diga onde estou errando.
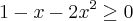
Resolvendo por Bhaskara chego nas raízes: x'=-1 e x"=1/2
Fatorando:
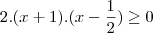
Aqui está o erro. O correto seria:
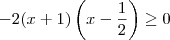
.
-

LuizAquino
- Colaborador Moderador - Professor

-
- Mensagens: 2654
- Registrado em: Sex Jan 21, 2011 09:11
- Localização: Teófilo Otoni - MG
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Mestrado - Modelagem Computacional
- Andamento: formado
-
 por renanrdaros » Sex Mar 25, 2011 16:23
por renanrdaros » Sex Mar 25, 2011 16:23
aaaaaaaaaahhhhhhhhhhhhhhhhhhhhhhhh mas eu sou buuuuuuuurro!!!!!!!!!!
-
renanrdaros
- Usuário Parceiro

-
- Mensagens: 54
- Registrado em: Sáb Mar 19, 2011 19:37
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Eng. de Computação
- Andamento: cursando
 por renanrdaros » Sex Mar 25, 2011 16:39
por renanrdaros » Sex Mar 25, 2011 16:39
Aproveitando o tópico... Tem outra inequação que não consegui resolver de jeito nenhum.

Resolvendo a expressão e analisando os dois casos possíveis, chego em uma inequação de 2º grau com
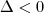
Como resolvo a partir daí? O resultado do livro não é vazio!
-
renanrdaros
- Usuário Parceiro

-
- Mensagens: 54
- Registrado em: Sáb Mar 19, 2011 19:37
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Eng. de Computação
- Andamento: cursando
 por MarceloFantini » Sex Mar 25, 2011 16:47
por MarceloFantini » Sex Mar 25, 2011 16:47
Não aproveite o tópico, crie um novo.
Futuro MATEMÁTICO
-
MarceloFantini
- Colaborador Moderador

-
- Mensagens: 3126
- Registrado em: Seg Dez 14, 2009 11:41
- Formação Escolar: GRADUAÇÃO
- Andamento: formado
 por renanrdaros » Sex Mar 25, 2011 18:08
por renanrdaros » Sex Mar 25, 2011 18:08
ok
-
renanrdaros
- Usuário Parceiro

-
- Mensagens: 54
- Registrado em: Sáb Mar 19, 2011 19:37
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Eng. de Computação
- Andamento: cursando
 por johnlaw » Dom Mar 27, 2011 14:18
por johnlaw » Dom Mar 27, 2011 14:18
Como você fatorou aquela equação ?
-
johnlaw
- Usuário Ativo

-
- Mensagens: 20
- Registrado em: Sex Ago 06, 2010 13:12
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Matemática Licenciatura
- Andamento: cursando
 por renanrdaros » Dom Mar 27, 2011 15:25
por renanrdaros » Dom Mar 27, 2011 15:25
www.vestibulandia.com.brDê uma olhada nas aulas de fatoração!
-
renanrdaros
- Usuário Parceiro

-
- Mensagens: 54
- Registrado em: Sáb Mar 19, 2011 19:37
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Eng. de Computação
- Andamento: cursando
 por johnlaw » Dom Mar 27, 2011 15:46
por johnlaw » Dom Mar 27, 2011 15:46
Já olhei... mas sei láh..
-
johnlaw
- Usuário Ativo

-
- Mensagens: 20
- Registrado em: Sex Ago 06, 2010 13:12
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Matemática Licenciatura
- Andamento: cursando
 por MarceloFantini » Dom Mar 27, 2011 16:15
por MarceloFantini » Dom Mar 27, 2011 16:15
Existe um teorema que diz que todo polinômio pode ser fatorado da maneira
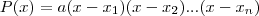
, onde
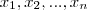
são as raízes (isto supõe raízes complexas também). Foi isto que ele usou.
Futuro MATEMÁTICO
-
MarceloFantini
- Colaborador Moderador

-
- Mensagens: 3126
- Registrado em: Seg Dez 14, 2009 11:41
- Formação Escolar: GRADUAÇÃO
- Andamento: formado
 por johnlaw » Dom Mar 27, 2011 16:35
por johnlaw » Dom Mar 27, 2011 16:35
Ah sim, descobre as raízes e substitui! Usamos ele tb quando temos as raízes e queremos saber a equação néh..
Valeu! Obrigado!
-
johnlaw
- Usuário Ativo

-
- Mensagens: 20
- Registrado em: Sex Ago 06, 2010 13:12
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Matemática Licenciatura
- Andamento: cursando
Voltar para Álgebra Elementar
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Resposta do livro errada ??
por Diego Math » Qui Jul 19, 2012 23:41
- 2 Respostas
- 2138 Exibições
- Última mensagem por DanielFerreira

Sex Jul 20, 2012 23:02
Geometria Plana
-
- ajuda, deu errada a resposta
por Guilhermme » Qua Mar 28, 2012 13:31
- 2 Respostas
- 3897 Exibições
- Última mensagem por ednaldo1982

Qua Mar 28, 2012 16:41
Sistemas de Equações
-
- [Vetores] Resposta errada?
por KleinIll » Qui Out 31, 2013 14:18
- 0 Respostas
- 941 Exibições
- Última mensagem por KleinIll

Qui Out 31, 2013 14:18
Geometria Analítica
-
- [Equação diferencial] Resposta não bate com o livro
por Bruno G Carneiro » Sex Mai 11, 2012 15:23
- 2 Respostas
- 3781 Exibições
- Última mensagem por Bruno G Carneiro

Ter Mai 15, 2012 18:18
Cálculo: Limites, Derivadas e Integrais
-
- Adição de Polinômios minha resposta diferente da do livro
por ravi » Ter Jan 31, 2012 14:02
- 2 Respostas
- 2253 Exibições
- Última mensagem por Arkanus Darondra

Ter Jan 31, 2012 14:49
Polinômios
Usuários navegando neste fórum: Nenhum usuário registrado e 3 visitantes
Assunto:
[Função] do primeiro grau e quadratica
Autor:
Thassya - Sáb Out 01, 2011 16:20
1) Para que os pontos (1,3) e (-3,1) pertençam ao grafico da função f(X)=ax + b ,o valor de b-a deve ser ?
2)Qual o maior valor assumido pela função f : [-7 ,10] em R definida por f(x) = x ao quadrado - 5x + 9?
3) A função f, do primeiro grau, é definida pos f(x)= 3x + k para que o gráfico de f corte o eixo das ordenadas no ponto de ordenada 5 é?
Assunto:
[Função] do primeiro grau e quadratica
Autor:
Neperiano - Sáb Out 01, 2011 19:46
Ola
Qual as suas dúvidas?
O que você não está conseguindo fazer?
Nos mostre para podermos ajudar
Atenciosamente
Assunto:
[Função] do primeiro grau e quadratica
Autor:
joaofonseca - Sáb Out 01, 2011 20:15
1)Dados dois pontos A=(1,3) e B=(-3,1) de uma reta, é possivel definir a sua equação.


Em

substitui-se
m, substitui-se
y e
x por um dos pares ordenados, e resolve-se em ordem a
b.

2)Na equação

não existem zeros.Senão vejamos
Completando o quadrado,

As coordenadas do vertice da parabola são

O eixo de simetria é a reta

.Como se pode observar o vertice está acima do eixo Ox, estando parabola virada para cima, o vertice é um mínimo absoluto.Então basta calcular a função para os valores dos extremos do intervalo.
f(-7)=93
f(10)=59
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
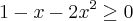
![\left(-\infty;-1 \right] \cup \left[\frac{1}{2};+\infty \right) \left(-\infty;-1 \right] \cup \left[\frac{1}{2};+\infty \right)](/latexrender/pictures/c29febe6c056dcd612e61c5a6dbc1b21.png)
![\left[-1;\frac{1}{2} \right] \left[-1;\frac{1}{2} \right]](/latexrender/pictures/9ff7930624f606598a07c05317984474.png)

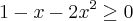
![\left(-\infty;-1 \right] \cup \left[\frac{1}{2};+\infty \right) \left(-\infty;-1 \right] \cup \left[\frac{1}{2};+\infty \right)](/latexrender/pictures/c29febe6c056dcd612e61c5a6dbc1b21.png)
![\left[-1;\frac{1}{2} \right] \left[-1;\frac{1}{2} \right]](/latexrender/pictures/9ff7930624f606598a07c05317984474.png)




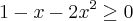
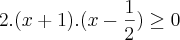
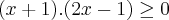
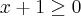
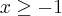
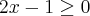
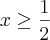
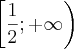
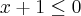
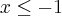
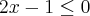
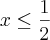
![\left(-\infty;-1 \right] \left(-\infty;-1 \right]](/latexrender/pictures/c4f642506d2ab8a8a9fc3234f7917fba.png)
![\left(-\infty;-1 \right] \left(-\infty;-1 \right]](/latexrender/pictures/c4f642506d2ab8a8a9fc3234f7917fba.png) U
U 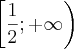

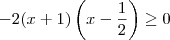 .
.


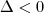






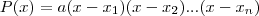 , onde
, onde 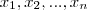 são as raízes (isto supõe raízes complexas também). Foi isto que ele usou.
são as raízes (isto supõe raízes complexas também). Foi isto que ele usou.




 substitui-se m, substitui-se y e x por um dos pares ordenados, e resolve-se em ordem a b.
substitui-se m, substitui-se y e x por um dos pares ordenados, e resolve-se em ordem a b.
 não existem zeros.Senão vejamos
não existem zeros.Senão vejamos

 .Como se pode observar o vertice está acima do eixo Ox, estando parabola virada para cima, o vertice é um mínimo absoluto.Então basta calcular a função para os valores dos extremos do intervalo.
.Como se pode observar o vertice está acima do eixo Ox, estando parabola virada para cima, o vertice é um mínimo absoluto.Então basta calcular a função para os valores dos extremos do intervalo.