 por Luza » Ter Mar 22, 2011 10:25
por Luza » Ter Mar 22, 2011 10:25
Por favor , alguém poderia me ajudar a fazer esse exercício ?
(a) A equa�cão 3lxl + 2lyl = 6 representa quatro segmentos que juntos formam um losango.
Encontre os v�ertices desse losango e as equações das retas, sem m�odulo, que formam os lados do losango.
Para isso, use as defi�ni�ções de lxl e lyl.
(b) Esboce a região formada pelos pontos (x; y) do plano que satisfaz a inequa�cão 3lxl + 2lyl � 6.
Para isso, use as defi�ni�ções de lxl e lyl.
(c) Encontre a �area da região do item (b), supondo que tanto no eixo x quanto eixo no y a unidade de
medida �é centi��metro.
-
Luza
- Novo Usuário

-
- Mensagens: 2
- Registrado em: Ter Mar 22, 2011 10:19
- Formação Escolar: GRADUAÇÃO
- Área/Curso: licenciatura
- Andamento: cursando
 por Luza » Ter Mar 22, 2011 22:40
por Luza » Ter Mar 22, 2011 22:40
Alguém ?
-
Luza
- Novo Usuário

-
- Mensagens: 2
- Registrado em: Ter Mar 22, 2011 10:19
- Formação Escolar: GRADUAÇÃO
- Área/Curso: licenciatura
- Andamento: cursando
 por MarceloFantini » Qua Mar 23, 2011 00:08
por MarceloFantini » Qua Mar 23, 2011 00:08
Lembre-se da definição de módulo:

se
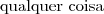
for

ou

se
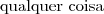
for

. Então, terá que avaliar quatro casos:
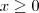
e

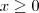
e

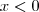
e

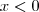
e

Veja as interseções, monte o gráfico e calcule a área.
Futuro MATEMÁTICO
-
MarceloFantini
- Colaborador Moderador

-
- Mensagens: 3126
- Registrado em: Seg Dez 14, 2009 11:41
- Formação Escolar: GRADUAÇÃO
- Andamento: formado
Voltar para Geometria Plana
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Área losango
 por Mi_chelle » Qui Mai 19, 2011 01:23
por Mi_chelle » Qui Mai 19, 2011 01:23
- 2 Respostas
- 2032 Exibições
- Última mensagem por Mi_chelle

Ter Mai 24, 2011 15:39
Geometria Plana
-
- Área do losango
por matway » Qui Set 08, 2011 14:22
- 1 Respostas
- 1635 Exibições
- Última mensagem por Neperiano

Qui Set 08, 2011 15:59
Trigonometria
-
- ÁREA DO LOSANGO
por L_lawliet » Qui Dez 08, 2011 23:01
- 4 Respostas
- 3001 Exibições
- Última mensagem por L_lawliet

Ter Dez 20, 2011 20:59
Geometria Plana
-
- Área do Losango
 por Ericka » Qua Jan 25, 2012 20:52
por Ericka » Qua Jan 25, 2012 20:52
- 2 Respostas
- 3744 Exibições
- Última mensagem por LuizAquino

Qua Jan 25, 2012 21:13
Geometria Plana
-
- Área do losango em malha
 por Ariel » Qua Nov 16, 2016 13:51
por Ariel » Qua Nov 16, 2016 13:51
- 0 Respostas
- 2633 Exibições
- Última mensagem por Ariel

Qua Nov 16, 2016 13:51
Geometria Plana
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
cálculo de limites
Autor:
Hansegon - Seg Ago 25, 2008 11:29
Bom dia.
Preciso de ajuda na solução deste problema, pois só chego ao resultado de 0 sobre 0.
Obrigado
\lim_{x\rightarrow-1} x³ +1/x²-1[/tex]
Assunto:
cálculo de limites
Autor:
Molina - Seg Ago 25, 2008 13:25

Realmente se você jogar o -1 na equação dá 0 sobre 0.
Indeterminações deste tipo você pode resolver por L'Hôpital
que utiliza derivada.
Outro modo é transformar o numerador e/ou denominador
para que não continue dando indeterminado.
Dica: dividir o numerador e o denominador por algum valor é uma forma que normalmente dá certo.

Caso ainda não tenha dado uma

, avisa que eu resolvo.
Bom estudo!
Assunto:
cálculo de limites
Autor:
Guill - Dom Abr 08, 2012 16:03



Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.


 se
se 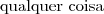 for
for  ou
ou  se
se  . Então, terá que avaliar quatro casos:
. Então, terá que avaliar quatro casos: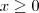 e
e 

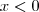 e
e 



 , avisa que eu resolvo.
, avisa que eu resolvo.

