![\int_{-1}^{3}[x]dx](/latexrender/pictures/5c0a6282f3363e09385571f01b651dbf.png "\int_{-1}^{3}[x]dx")
e diz que [x] representa um inteiro menor ou igual a x.Entendi o gráfico da função escada que fica assim http://www.wolframalpha.com/input/?i=in ... rt+of+x%29 somando as áreas dá 2. Mas a resposta não precisa do gráfico, ou pelo menos esta dizendo para calcular sem mencionar o gráfico.
Então sem o gráfico: entendi que tem que "jogar" -1 e 3 no x, daí vem a sequência -1, 0, 1, 2 e 3 que são os valores que a função assume nesse intervalo. Depois disso, seguindo o raciocínio do Apostol, tem que visualizar as partições (segmentos como no gráfico aí em cima). Assumindo que é uma função f(x) = x (o gráfico fica sendo a reta que passa pela origem e tem y = x para todos os pontos, vi isso com o grupo de estudos. Da reta da função vem os pontos da função escada, fechada a esquerda e aberta a direita). A parte mais complicada esta sendo a notação. Os intervalos, por exemplo o primeiro, fica
. A função vale -1 nesse ponto e tem "base da partição" -1 tambem. Daí a soma, tem o símbolo da somatória, ou o professor disse q tb pode escrever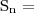 
. As partições escreve base x altura ou altura x base, tanto faz? Na notação do grupo de estudos ficou 
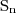= -1 . (0 -(-1)) + 0 . (-1 . 0) + 1 . (2 - 1) + 2 . (3 - 2)Sobre o Apostol: até essa parte de funções fáceis de integrar esta bem, nada muito dificil.
.
em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto.
o ângulo entre o eixo horizontal e o afixo 
. O triângulo é retângulo com catetos 
e 
, tal que 
. Seja 
o ângulo complementar. Então 
. Como 
, o ângulo que o afixo 
formará com a horizontal será 
, então 
. Como módulo é um: 
.
.