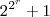 é um número primo para
é um número primo para 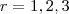 ou
ou  , mas não é para
, mas não é para  . Quantos fatores primos tem o número
. Quantos fatores primos tem o número 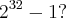
Obs: Percebi que a expressão
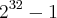 é a diferença de dois quadrados, transformei para
é a diferença de dois quadrados, transformei para 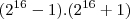 . Transformei
. Transformei  em
em 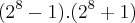 .
.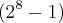 dá como resultado
dá como resultado 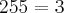 x
x x
x e
e 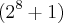 dá como resultado 257, que é primo. Logo tenho que
dá como resultado 257, que é primo. Logo tenho que  tem 4 números primos... agora fica a minha dúvida, como posso saber se
tem 4 números primos... agora fica a minha dúvida, como posso saber se  é primo ou não? (Lembrando que eu devo fazer questões dessa, futuramente, só com lápis, papel e borracha... a prova OBM)!
é primo ou não? (Lembrando que eu devo fazer questões dessa, futuramente, só com lápis, papel e borracha... a prova OBM)!

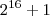 ) é primo ou não?
) é primo ou não?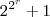 é um número primo para r= 1, 2, 3 ou 4, mas não é para 5".
é um número primo para r= 1, 2, 3 ou 4, mas não é para 5".