então eu estou fazendo uns exercicios so que sempre da erro -.-, sera que voces poderiam me dar uma luz?!
postarei os primeiros exercicios aqui, e gostaria que voces me indicacem o erro para que eu possa corrigir-los, ;/
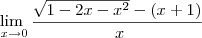
Nesse exercicio eu estou fazendo o conjugado, pela equação de cima, e estou caindo aqui:
(Desculpa nao colocar o passo a passo eh que ainda sou leigo quanto ao programa)
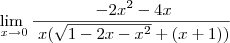
entao pessoal dai pra frente eu nao sei o que fazer, pois o resultado esta dando -2.
outro exercicio, esse eu nao tenho ideia de como começar,:
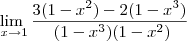
Desde ja agradeço a todos


 em evidência no numerador e veja o que acontece. Não tentei o segundo, mas procure usar que
em evidência no numerador e veja o que acontece. Não tentei o segundo, mas procure usar que 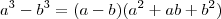 e
e 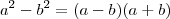 .
.

 .
. ,
,  e para
e para  ,
,  .
.
 e
e  , monte a função e substitua
, monte a função e substitua  por
por  .
.
