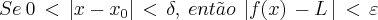
O seguinte limite:
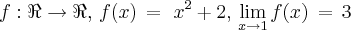
Consegui demonstrar o seguinte:
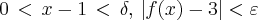
Logo,
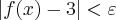
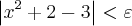
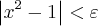
![\left[\left(x+1 \right)\left(x-1 \right) \right]<\varepsilon \left[\left(x+1 \right)\left(x-1 \right) \right]<\varepsilon](/latexrender/pictures/d1398814707f6526d9bcfc36ff5080a5.png)
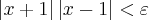
A partir daí, não consegui desenvolver o resto do problema.
No livro, tem um problema parecido com esse e que possui a resolução. Ele falava de
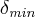 , mas não entendi.
, mas não entendi.Obrigada pela atenção.

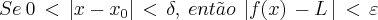
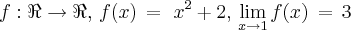
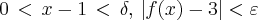
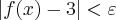
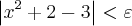
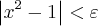
![\left[\left(x+1 \right)\left(x-1 \right) \right]<\varepsilon \left[\left(x+1 \right)\left(x-1 \right) \right]<\varepsilon](/latexrender/pictures/d1398814707f6526d9bcfc36ff5080a5.png)
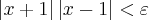
 , mas não entendi.
, mas não entendi.
jessicaccs escreveu:No livro, tem um problema parecido com esse e que possui a resolução. Ele falava de, mas não entendi.
 , nós teremos que |x-1| <
, nós teremos que |x-1| < 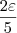 . Mas, nós havíamos delimitado que |x-1| < 1/2.
. Mas, nós havíamos delimitado que |x-1| < 1/2. =1/2 ou
=1/2 ou 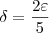 ?
? 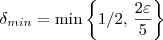 .
.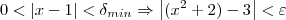

Voltar para Cálculo: Limites, Derivadas e Integrais
Usuários navegando neste fórum: Nenhum usuário registrado e 8 visitantes
 em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto.
em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto. o ângulo entre o eixo horizontal e o afixo
o ângulo entre o eixo horizontal e o afixo  . O triângulo é retângulo com catetos
. O triângulo é retângulo com catetos  e
e  , tal que
, tal que  . Seja
. Seja  o ângulo complementar. Então
o ângulo complementar. Então  . Como
. Como  , o ângulo que o afixo
, o ângulo que o afixo  formará com a horizontal será
formará com a horizontal será  , mas negativo pois tem de ser no quarto quadrante. Se
, mas negativo pois tem de ser no quarto quadrante. Se  , então
, então  . Como módulo é um:
. Como módulo é um:  .
. .
.