 por fernandocez » Sáb Mar 19, 2011 18:50
por fernandocez » Sáb Mar 19, 2011 18:50
Fui cheio de vontade prá resolver, achando que era facinho. E não saí do lugar. Preciso de uma dica.
27. Sejam x e y números reais, tais que x + y = 3 e x² + y² = 19. Valor X³ + y³ é:
resp: 72
Eu tentei colocar dentro de raiz, tentei produtos notáveis, descobri que não tem haver. Aguardo uma dica.
Editado pela última vez por
fernandocez em Seg Mar 21, 2011 00:07, em um total de 1 vez.
-

fernandocez
- Colaborador Voluntário

-
- Mensagens: 131
- Registrado em: Seg Fev 14, 2011 15:01
- Localização: São João de Meriti - RJ
- Formação Escolar: GRADUAÇÃO
- Área/Curso: licenciatura em matemática
- Andamento: formado
 por LuizAquino » Sáb Mar 19, 2011 19:07
por LuizAquino » Sáb Mar 19, 2011 19:07
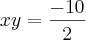
Dica(i)
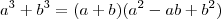
(ii) Elevando ambos os membros da equação
x+y=3 ao quadrado e usando que
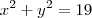
, você é capaz de obter quanto é
xy.
-

LuizAquino
- Colaborador Moderador - Professor

-
- Mensagens: 2654
- Registrado em: Sex Jan 21, 2011 09:11
- Localização: Teófilo Otoni - MG
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Mestrado - Modelagem Computacional
- Andamento: formado
-
Voltar para Funções
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Questão prova concurso (função)
por fernandocez » Qui Mar 10, 2011 22:17
- 6 Respostas
- 2695 Exibições
- Última mensagem por fernandocez

Sex Mar 11, 2011 11:17
Funções
-
- Questão prova concurso função 1
por fernandocez » Ter Mar 22, 2011 09:28
- 6 Respostas
- 2655 Exibições
- Última mensagem por fernandocez

Ter Mar 22, 2011 12:45
Funções
-
- Questão prova concurso
por fernandocez » Sáb Fev 26, 2011 19:10
- 6 Respostas
- 3553 Exibições
- Última mensagem por fernandocez

Sáb Fev 26, 2011 22:29
Geometria Plana
-
- Questão prova concurso
por fernandocez » Sáb Fev 26, 2011 23:27
- 3 Respostas
- 2497 Exibições
- Última mensagem por fernandocez

Dom Fev 27, 2011 10:33
Funções
-
- Questão prova concurso (sen e cos)
por fernandocez » Qua Mar 02, 2011 11:26
- 13 Respostas
- 9273 Exibições
- Última mensagem por fernandocez

Dom Mar 13, 2011 12:18
Trigonometria
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
Exercicios de polinomios
Autor:
shaft - Qua Jun 30, 2010 17:30

Então, o exercicio pede para encontrar

.
Bom, tentei resolver a questão acima desenvolvendo as duas partes em ( )...Logo dps cheguei em um resultado q nao soube o q fazer mais.
Se vcs puderem ajudar !
Assunto:
Exercicios de polinomios
Autor:
Douglasm - Qua Jun 30, 2010 17:53
Bom, se desenvolvermos isso, encontramos:

Para que os polinômios sejam iguais, seus respectivos coeficientes devem ser iguais (ax = bx ; ax² = bx², etc.):


Somando a primeira e a segunda equação:

Finalmente:

Até a próxima.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.


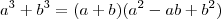
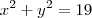 , você é capaz de obter quanto é
, você é capaz de obter quanto é 
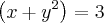

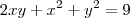
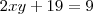

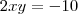






 .
.



