Oi pessoal, mais uma que não consegui resolver. Vamos a questão.
37. Três números positivos formam uma progressão aritimética crescente. A soma desses três números é 18. Mantendo-se os dois menores e acrescentando-se 8 unidades ao maior, fica formada uma progressão geométrica. O produto dos três números dados inicialmente é:
resp: 120
1ª Eu fiz assim.
PA(x-r, x, x+r)
x-r + x + x+r = 18
x = 6
2ª Eu fui pela resposta:
(x-r)x(x+r) = 120 (resposta)
(x² - r²)x = 120
36 - r² = 20
r = 4
PG(2, 6, 18)
Será que existe um modo de fazer sem ir pelas opções? Visto que no concurso o tempo é pouco.
forma uma p.g. com termos não nulos, então 
.
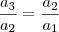![\frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}}](/latexrender/pictures/981987c7bcdf9f8f498ca4605785636a.png "\frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}}")
![\sqrt[]{2}](/latexrender/pictures/f21662d1cabab6e8b273a4b6f1cd663a.png "\sqrt[]{2}")
e elevar ao quadrado os dois lados)