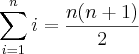




 (essa incógnita é a mais comum), por último, tens que demonstrar, algebricamente, que a fórmula
(essa incógnita é a mais comum), por último, tens que demonstrar, algebricamente, que a fórmula 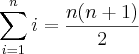 vale para
vale para  .
. 


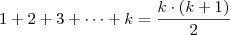
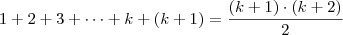
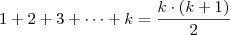 podemos fazer uma substituição no lado esquerdo da igualdade, logo teremos:
podemos fazer uma substituição no lado esquerdo da igualdade, logo teremos: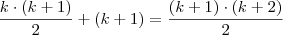


Usuários navegando neste fórum: Nenhum usuário registrado e 0 visitantes


 , avisa que eu resolvo.
, avisa que eu resolvo.

