 por jessicaccs » Ter Mar 08, 2011 19:55
por jessicaccs » Ter Mar 08, 2011 19:55
Boa noite,
gostaria de ajuda nessa questão:
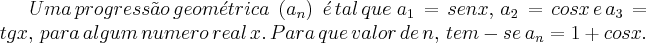
As alternativas são:
a) 4 b) 5 c) 6 d) 7 e) 8
Tentei resolvê-la através da propriedade da PG que diz que um termo médio de dois equidistantes deste é a média geométrica dos dois números.
Entretanto, não consegui resolver.
Obrigada,
Jéssica.
-
jessicaccs
- Novo Usuário

-
- Mensagens: 8
- Registrado em: Ter Out 13, 2009 19:13
- Formação Escolar: ENSINO MÉDIO
- Área/Curso: Efomm
- Andamento: cursando
 por LuizAquino » Qua Mar 09, 2011 21:28
por LuizAquino » Qua Mar 09, 2011 21:28
Sabemos que em uma p.g. é válido que

, com
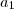
e

não nulos. Disso, nós obtemos que:



(vamos identificar essa equação como (a))
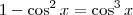
Dividindo tudo por

:

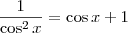
(vamos identificar essa equação como (b))
Sabemos que o termo geral de uma p.g. é dado por
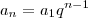
, onde
q é a razão. Desse modo, temos que
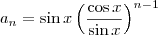
.
Nós queremos determinar
n tal que

.
Note que para
n=8, nós temos que:
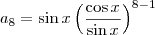
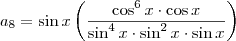
Usando a equação (a) e fazendo as simplificações necessárias, nós obtemos:

Agora, usando a equação (b) concluímos que o número
n procurado é 8.
-

LuizAquino
- Colaborador Moderador - Professor

-
- Mensagens: 2654
- Registrado em: Sex Jan 21, 2011 09:11
- Localização: Teófilo Otoni - MG
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Mestrado - Modelagem Computacional
- Andamento: formado
-
 por jessicaccs » Qua Mar 09, 2011 22:18
por jessicaccs » Qua Mar 09, 2011 22:18
Obrigada pela resolução, Luiz.
Só gostaria que você tirasse uma dúvida que fiquei.
Por que você adotou o número 8 dentre tantos outros que poderiam ser?
Obrigada.
-
jessicaccs
- Novo Usuário

-
- Mensagens: 8
- Registrado em: Ter Out 13, 2009 19:13
- Formação Escolar: ENSINO MÉDIO
- Área/Curso: Efomm
- Andamento: cursando
 por LuizAquino » Qua Mar 09, 2011 23:31
por LuizAquino » Qua Mar 09, 2011 23:31
jessicaccs escreveu:Por que você adotou o número 8 dentre tantos outros que poderiam ser?
Nesse caso eu adotei
n = 8 devido as opções dadas no gabarito. Mas, poderíamos ter feito de outra maneira.
Nós queremos determinar
n tal que

.
Lembrando-se das equações (a) e (b), nós podemos armar a seguinte equação exponencial (na qual a base é

):
![(\cos x)^{\frac{3}{2}} \left[\frac{\cos x}{(\cos x)^{\frac{3}{2}}}\right]^{n-1} = (\cos x)^{-2} (\cos x)^{\frac{3}{2}} \left[\frac{\cos x}{(\cos x)^{\frac{3}{2}}}\right]^{n-1} = (\cos x)^{-2}](/latexrender/pictures/08df63b8b622d55869938e6d324d1671.png)

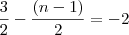 n = 8
n = 8
-

LuizAquino
- Colaborador Moderador - Professor

-
- Mensagens: 2654
- Registrado em: Sex Jan 21, 2011 09:11
- Localização: Teófilo Otoni - MG
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Mestrado - Modelagem Computacional
- Andamento: formado
-
 por jessicaccs » Sex Mar 11, 2011 16:22
por jessicaccs » Sex Mar 11, 2011 16:22
Obrigada, Luiz Aquino.

-
jessicaccs
- Novo Usuário

-
- Mensagens: 8
- Registrado em: Ter Out 13, 2009 19:13
- Formação Escolar: ENSINO MÉDIO
- Área/Curso: Efomm
- Andamento: cursando
Voltar para Progressões
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
(FGV) ... função novamente rs
Autor:
my2009 - Qua Dez 08, 2010 21:48
Uma função polinomial f do 1° grau é tal que f(3) = 6 e f(4) = 8.Portanto o valor de f(10) é :
Assunto:
(FGV) ... função novamente rs
Autor: Anonymous - Qui Dez 09, 2010 17:25
Uma função de 1º grau é dada por

.
Temos que para

,

e para

,

.

Ache o valor de

e

, monte a função e substitua

por

.
Assunto:
(FGV) ... função novamente rs
Autor:
Pinho - Qui Dez 16, 2010 13:57
my2009 escreveu:Uma função polinomial f do 1° grau é tal que f(3) = 6 e f(4) = 8.Portanto o valor de f(10) é :
f(x)= 2.x
f(3)=2.3=6
f(4)=2.4=8
f(10)=2.10=20
Assunto:
(FGV) ... função novamente rs
Autor:
dagoth - Sex Dez 17, 2010 11:55
isso ai foi uma questao da FGV?
haahua to precisando trocar de faculdade.
Assunto:
(FGV) ... função novamente rs
Autor:
Thiago 86 - Qua Mar 06, 2013 23:11
Saudações!

ví suaquestão e tentei resolver, depois você conta-me se eu acertei.
Uma função de 1º grau é dada por y=3a+b
Resposta :
3a+b=6 x(4)
4a+b=8 x(-3)
12a+4b=24
-12a-3b=-24
b=0
substituindo b na 1°, ttenho que: 3a+b=6
3a+0=6
a=2
substituindo em: y=3a+b
y=30+0
y=30

Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
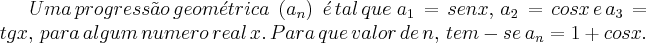


 , com
, com 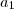 e
e  não nulos. Disso, nós obtemos que:
não nulos. Disso, nós obtemos que:

 (vamos identificar essa equação como (a))
(vamos identificar essa equação como (a))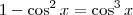
 :
:
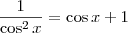 (vamos identificar essa equação como (b))
(vamos identificar essa equação como (b))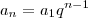 , onde
, onde 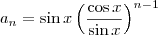 .
. .
.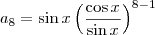
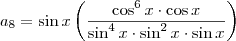


 ):
):![(\cos x)^{\frac{3}{2}} \left[\frac{\cos x}{(\cos x)^{\frac{3}{2}}}\right]^{n-1} = (\cos x)^{-2} (\cos x)^{\frac{3}{2}} \left[\frac{\cos x}{(\cos x)^{\frac{3}{2}}}\right]^{n-1} = (\cos x)^{-2}](/latexrender/pictures/08df63b8b622d55869938e6d324d1671.png)

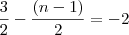
 .
. ,
,  e para
e para  ,
,  .
.
 e
e  , monte a função e substitua
, monte a função e substitua  por
por  .
.
