 por johnlaw » Sáb Mar 05, 2011 18:15
por johnlaw » Sáb Mar 05, 2011 18:15
Olá Pessoal,
Como posso demonstrar que

Obrigado
Abraços!
-
johnlaw
- Usuário Ativo

-
- Mensagens: 20
- Registrado em: Sex Ago 06, 2010 13:12
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Matemática Licenciatura
- Andamento: cursando
 por MarceloFantini » Sáb Mar 05, 2011 19:26
por MarceloFantini » Sáb Mar 05, 2011 19:26
John, poderia mostrar o problema completo? Assim está estranho. De qualquer forma, poderia tentar demonstrar que

ou

.
Futuro MATEMÁTICO
-
MarceloFantini
- Colaborador Moderador

-
- Mensagens: 3126
- Registrado em: Seg Dez 14, 2009 11:41
- Formação Escolar: GRADUAÇÃO
- Andamento: formado
 por Abelardo » Seg Mar 07, 2011 01:04
por Abelardo » Seg Mar 07, 2011 01:04
Como

então extraindo a raiz quadrada de ambos os membros terás que

.
Afirmação: ''a é igual a b''. ''b'' será igual a ''a'' , logo os seus quadrados serão iguais.
-

Abelardo
- Colaborador Voluntário

-
- Mensagens: 159
- Registrado em: Qui Mar 03, 2011 01:45
- Formação Escolar: ENSINO MÉDIO
- Andamento: cursando
 por MarceloFantini » Seg Mar 07, 2011 13:05
por MarceloFantini » Seg Mar 07, 2011 13:05
A rigor, extraindo as raízes quadradas você encontra que os
módulos são iguais:
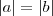
, e que então temos dois casos:

ou

. Só podemos afirmar que é o primeiro se for dito que
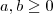
.
Futuro MATEMÁTICO
-
MarceloFantini
- Colaborador Moderador

-
- Mensagens: 3126
- Registrado em: Seg Dez 14, 2009 11:41
- Formação Escolar: GRADUAÇÃO
- Andamento: formado
 por johnlaw » Seg Mar 07, 2011 18:02
por johnlaw » Seg Mar 07, 2011 18:02
Acho que descobri,
Estava pensando em:
Se

, então

ou

Se

, então são iguais, se são iguais, então

= 0
Sabemos que,

(que é zero) também é igual a

então:
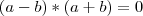
e se isso aí é zero então:
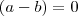
ou

Para
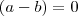
temos:

e
para
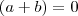
temos:

É isso que estava eu querendo, provar que

, mas que na verdade tenho que provar as duas hipóteses:

e

-
johnlaw
- Usuário Ativo

-
- Mensagens: 20
- Registrado em: Sex Ago 06, 2010 13:12
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Matemática Licenciatura
- Andamento: cursando
 por Abelardo » Seg Mar 07, 2011 18:28
por Abelardo » Seg Mar 07, 2011 18:28
Foi lindo isso! Aprendi demais com essa..
-

Abelardo
- Colaborador Voluntário

-
- Mensagens: 159
- Registrado em: Qui Mar 03, 2011 01:45
- Formação Escolar: ENSINO MÉDIO
- Andamento: cursando
 por MarceloFantini » Seg Mar 07, 2011 20:34
por MarceloFantini » Seg Mar 07, 2011 20:34
Você está confundindo as palavras. Você não tem que provar hipóteses. Eu mesmo não estou entendendo até agora o que exatamente você quer: era provar que dados dois números a e b,

?
Futuro MATEMÁTICO
-
MarceloFantini
- Colaborador Moderador

-
- Mensagens: 3126
- Registrado em: Seg Dez 14, 2009 11:41
- Formação Escolar: GRADUAÇÃO
- Andamento: formado
 por johnlaw » Qui Mar 10, 2011 14:40
por johnlaw » Qui Mar 10, 2011 14:40
Me desculpe se me enganei com as palavras...
Eu queria provar que

e para isso eu caio em duas hipóteses (está correto o termo ?):

e

então.. provar essas duas últimas... que foi o que fiz..
Abraços!
-
johnlaw
- Usuário Ativo

-
- Mensagens: 20
- Registrado em: Sex Ago 06, 2010 13:12
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Matemática Licenciatura
- Andamento: cursando
 por MarceloFantini » Qui Mar 10, 2011 19:58
por MarceloFantini » Qui Mar 10, 2011 19:58
Não, você está confundindo ainda. Se você saiu que

, isso é sua hipótese. Se você chegou que

ou

, isso é sua tese.
Até agora você não postou a questão na íntegra.
Futuro MATEMÁTICO
-
MarceloFantini
- Colaborador Moderador

-
- Mensagens: 3126
- Registrado em: Seg Dez 14, 2009 11:41
- Formação Escolar: GRADUAÇÃO
- Andamento: formado
 por johnlaw » Sex Mar 11, 2011 01:43
por johnlaw » Sex Mar 11, 2011 01:43
Ah sim.. é isso, eu queria provar essa hipótese e consegui. Só isso, não tem questão.
Obrigado, abraços!
-
johnlaw
- Usuário Ativo

-
- Mensagens: 20
- Registrado em: Sex Ago 06, 2010 13:12
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Matemática Licenciatura
- Andamento: cursando
Voltar para Álgebra Elementar
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Igualdade de números complexos - Duvida em exercicio
por DonTLie » Qui Mar 11, 2010 17:23
- 4 Respostas
- 16014 Exibições
- Última mensagem por MarceloFantini

Sex Mar 12, 2010 17:40
Tópicos sem Interação (leia as regras)
-
- duvidas dois numeros irracionais
por hevhoram » Qui Jun 24, 2010 11:56
- 2 Respostas
- 2480 Exibições
- Última mensagem por MarceloFantini

Qui Jun 24, 2010 14:03
Álgebra Elementar
-
- Razão entre dois números
por lucas7 » Qui Fev 24, 2011 21:21
- 1 Respostas
- 2083 Exibições
- Última mensagem por lucas7

Sex Fev 25, 2011 08:44
Sistemas de Equações
-
- Maior entre dois numeros
por TiagoRodrigues » Qui Mar 01, 2012 14:37
- 5 Respostas
- 3927 Exibições
- Última mensagem por TiagoRodrigues

Sex Mar 02, 2012 11:18
Sistemas de Equações
-
- Sequência recursiva da média de dois números
por ant_dii » Qua Jun 29, 2011 20:40
- 0 Respostas
- 1763 Exibições
- Última mensagem por ant_dii

Qua Jun 29, 2011 20:40
Sequências
Usuários navegando neste fórum: Nenhum usuário registrado e 2 visitantes
Assunto:
Unesp - 95 Números Complexos
Autor:
Alucard014 - Dom Ago 01, 2010 18:22
(UNESP - 95) Seja L o Afixo de um Número complexo

em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto.
Assunto:
Unesp - 95 Números Complexos
Autor:
MarceloFantini - Qui Ago 05, 2010 17:27
Seja

o ângulo entre o eixo horizontal e o afixo

. O triângulo é retângulo com catetos

e

, tal que

. Seja

o ângulo complementar. Então

. Como

, o ângulo que o afixo

formará com a horizontal será

, mas negativo pois tem de ser no quarto quadrante. Se

, então

. Como módulo é um:

.
Logo, o afixo é

.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.




 ou
ou  .
.

 então extraindo a raiz quadrada de ambos os membros terás que
então extraindo a raiz quadrada de ambos os membros terás que  .
.
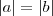 , e que então temos dois casos:
, e que então temos dois casos:  ou
ou  . Só podemos afirmar que é o primeiro se for dito que
. Só podemos afirmar que é o primeiro se for dito que 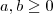 .
.

 , então
, então  ou
ou 
 , então são iguais, se são iguais, então
, então são iguais, se são iguais, então  = 0
= 0 (que é zero) também é igual a
(que é zero) também é igual a  então:
então: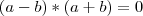 e se isso aí é zero então:
e se isso aí é zero então: 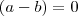 ou
ou 
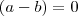 temos:
temos:  e
e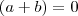 temos:
temos: 
 , mas que na verdade tenho que provar as duas hipóteses:
, mas que na verdade tenho que provar as duas hipóteses:  e
e 


 ?
?

 e para isso eu caio em duas hipóteses (está correto o termo ?):
e para isso eu caio em duas hipóteses (está correto o termo ?):  e
e  então.. provar essas duas últimas... que foi o que fiz..
então.. provar essas duas últimas... que foi o que fiz.. 
 , isso é sua hipótese. Se você chegou que
, isso é sua hipótese. Se você chegou que  ou
ou  , isso é sua tese.
, isso é sua tese.


 em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto.
em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto. o ângulo entre o eixo horizontal e o afixo
o ângulo entre o eixo horizontal e o afixo  . O triângulo é retângulo com catetos
. O triângulo é retângulo com catetos  e
e  , tal que
, tal que  . Seja
. Seja  o ângulo complementar. Então
o ângulo complementar. Então  . Como
. Como  , o ângulo que o afixo
, o ângulo que o afixo  formará com a horizontal será
formará com a horizontal será  , mas negativo pois tem de ser no quarto quadrante. Se
, mas negativo pois tem de ser no quarto quadrante. Se  , então
, então  . Como módulo é um:
. Como módulo é um:  .
. .
.