 por Regina » Seg Mar 07, 2011 15:09
por Regina » Seg Mar 07, 2011 15:09
Alguém me explica como é que saio daqui??
Tenho que saber o conjunto solução de
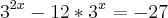
Eu desenvolvi assim:
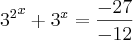
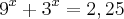
E agora como saio daqui? se 3 e 9 estivessem a multiplicar era fácil, mas estão a somar. Já tentei também fazer os logaritmos mas não dá o resultado correcto.
-
Regina
- Usuário Ativo

-
- Mensagens: 17
- Registrado em: Sex Fev 25, 2011 14:31
- Formação Escolar: ENSINO MÉDIO PROFISSIONALIZANTE
- Área/Curso: curso técnico em química
- Andamento: cursando
 por Pedro123 » Seg Mar 07, 2011 15:26
por Pedro123 » Seg Mar 07, 2011 15:26
Fala regina, seguinte, nesse tipo de questão, tente usar o artificio a seguir:
temos a equação
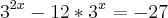
Faça algo do tipo

, pois assim cairá em uma equação do segundo grau, achando o

, iguale-o à

, se for o caso usando logaritmos, que assim você encontrará o x.
qualquer duvida é só perguntar, abraços
-
Pedro123
- Usuário Parceiro

-
- Mensagens: 60
- Registrado em: Qui Jun 10, 2010 22:46
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Mecanica - 1° Período
- Andamento: cursando
Voltar para Logaritmos
Usuários navegando neste fórum: Nenhum usuário registrado e 0 visitantes
Assunto:
cálculo de limites
Autor:
Hansegon - Seg Ago 25, 2008 11:29
Bom dia.
Preciso de ajuda na solução deste problema, pois só chego ao resultado de 0 sobre 0.
Obrigado
\lim_{x\rightarrow-1} x³ +1/x²-1[/tex]
Assunto:
cálculo de limites
Autor:
Molina - Seg Ago 25, 2008 13:25

Realmente se você jogar o -1 na equação dá 0 sobre 0.
Indeterminações deste tipo você pode resolver por L'Hôpital
que utiliza derivada.
Outro modo é transformar o numerador e/ou denominador
para que não continue dando indeterminado.
Dica: dividir o numerador e o denominador por algum valor é uma forma que normalmente dá certo.

Caso ainda não tenha dado uma

, avisa que eu resolvo.
Bom estudo!
Assunto:
cálculo de limites
Autor:
Guill - Dom Abr 08, 2012 16:03



Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
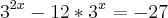
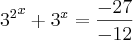
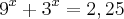

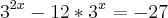
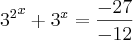
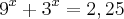

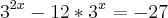
 , pois assim cairá em uma equação do segundo grau, achando o
, pois assim cairá em uma equação do segundo grau, achando o  , iguale-o à
, iguale-o à  , se for o caso usando logaritmos, que assim você encontrará o x.
, se for o caso usando logaritmos, que assim você encontrará o x.


 , avisa que eu resolvo.
, avisa que eu resolvo.

