 por fernandocez » Dom Mar 06, 2011 12:34
por fernandocez » Dom Mar 06, 2011 12:34
Caros amigos mais uma questão que tentei e não consegui resolver.
50. Considere todos os valores reais de x e y que satisfazem a equação
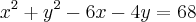
. O maior valor possível de y é:
resp.: 11
Eu não sabia como fazer, fiz assim:
Usei a equação da circunferência: x²+y²-2ax-2ay+(a²+b²-r²) =
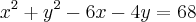
Encotrei:
a=3
b=2
r=9
Desenhei o gráfico e pensei que tinha alguma ligação com círculo quando passa no maior ponto de y. Tem a ver? Aguardo uma ajuda.
-

fernandocez
- Colaborador Voluntário

-
- Mensagens: 131
- Registrado em: Seg Fev 14, 2011 15:01
- Localização: São João de Meriti - RJ
- Formação Escolar: GRADUAÇÃO
- Área/Curso: licenciatura em matemática
- Andamento: formado
 por MarceloFantini » Dom Mar 06, 2011 12:57
por MarceloFantini » Dom Mar 06, 2011 12:57
Sim, o maior valor de y será o valor do centro mais o raio, que é o ponto mais alto da circunferência. Assim,
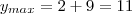
. Se ele pedisse o mínimo, seria o centro menos o raio. Se ele pedisse mais afastado em x, seria o equivalente só que usando coordenadas do x.
Futuro MATEMÁTICO
-
MarceloFantini
- Colaborador Moderador

-
- Mensagens: 3126
- Registrado em: Seg Dez 14, 2009 11:41
- Formação Escolar: GRADUAÇÃO
- Andamento: formado
 por LuizAquino » Dom Mar 06, 2011 12:59
por LuizAquino » Dom Mar 06, 2011 12:59
DicaNote que a equação
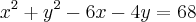
é a mesma que
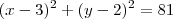
.
-

LuizAquino
- Colaborador Moderador - Professor

-
- Mensagens: 2654
- Registrado em: Sex Jan 21, 2011 09:11
- Localização: Teófilo Otoni - MG
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Mestrado - Modelagem Computacional
- Andamento: formado
-
 por fernandocez » Dom Mar 06, 2011 13:58
por fernandocez » Dom Mar 06, 2011 13:58
Fantini escreveu:Sim, o maior valor de y será o valor do centro mais o raio, que é o ponto mais alto da circunferência. Assim,
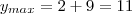
. Se ele pedisse o mínimo, seria o centro menos o raio. Se ele pedisse mais afastado em x, seria o equivalente só que usando coordenadas do x.
Valeu amigo, agora vendo o gráfico ficou claro. Eu até desenhei quase isso, mas nem sempre o que parece é.
-

fernandocez
- Colaborador Voluntário

-
- Mensagens: 131
- Registrado em: Seg Fev 14, 2011 15:01
- Localização: São João de Meriti - RJ
- Formação Escolar: GRADUAÇÃO
- Área/Curso: licenciatura em matemática
- Andamento: formado
 por fernandocez » Dom Mar 06, 2011 14:06
por fernandocez » Dom Mar 06, 2011 14:06
LuizAquino escreveu:DicaNote que a equação
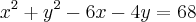
é a mesma que
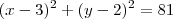
.
Oi Luiz, eu "simplifiquei" a expressão e realmente são iguais mas vc poderia dizer a relação com o problema que acredito ser importante prá minha aprendizagem. Visto que tenho que aprender muita coisa prá passar nesse concurso ou nos próximos que virá.
-

fernandocez
- Colaborador Voluntário

-
- Mensagens: 131
- Registrado em: Seg Fev 14, 2011 15:01
- Localização: São João de Meriti - RJ
- Formação Escolar: GRADUAÇÃO
- Área/Curso: licenciatura em matemática
- Andamento: formado
 por Renato_RJ » Dom Mar 06, 2011 14:22
por Renato_RJ » Dom Mar 06, 2011 14:22
fernandocez escreveu:LuizAquino escreveu:DicaNote que a equação
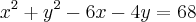
é a mesma que
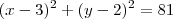
.
Oi Luiz, eu "simplifiquei" a expressão e realmente são iguais mas vc poderia dizer a relação com o problema que acredito ser importante prá minha aprendizagem. Visto que tenho que aprender muita coisa prá passar nesse concurso ou nos próximos que virá.
Grande Fernando... Tudo em paz ??
Campeão, veja, o Luiz simplificou a equação da circunferência para a sua forma reduzida da onde podemos retirar os valores da coordenada do centro e do raio, veja:
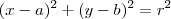
Logo, as coordenadas do centro serão:

O raio será a raiz quadrada de 81, isto é, 9...
Espero ter ajudado..
[ ]'s
Renato.
Iniciando a minha "caminhada" pela matemática agora... Tenho muito o quê aprender...
-

Renato_RJ
- Colaborador Voluntário

-
- Mensagens: 306
- Registrado em: Qui Jan 06, 2011 15:47
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Mestrado em Matemática
- Andamento: cursando
 por LuizAquino » Dom Mar 06, 2011 17:10
por LuizAquino » Dom Mar 06, 2011 17:10
Renato_RJ escreveu: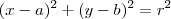
Logo, as coordenadas do centro serão:
C = (-a, -b)
Correção: as coordenadas do centro são
C = (a, b).
Por exemplo, na equação
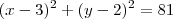
o centro é
C=(3, 2). Note que
a = 3 e
b = 2 nesse caso.
Para usar a definição do jeito que você disse, então deveria ser:
Na equação geral
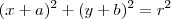
, o centro é
C=(-a, -b). No exemplo da equação acima, que pode ser escrita como
![[x+(-3)]^{2}+[y+(-2)]^{2} = 81 [x+(-3)]^{2}+[y+(-2)]^{2} = 81](/latexrender/pictures/cdd57000c68898d5d4812b31d0d3aab7.png)
, teríamos
a = -3 e
b = -2. Novamente o centro será
C=(-(-3), -(-2)) = (3, 2).
-

LuizAquino
- Colaborador Moderador - Professor

-
- Mensagens: 2654
- Registrado em: Sex Jan 21, 2011 09:11
- Localização: Teófilo Otoni - MG
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Mestrado - Modelagem Computacional
- Andamento: formado
-
Voltar para Geometria Analítica
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Questão prova concurso
por fernandocez » Sáb Fev 26, 2011 19:10
- 6 Respostas
- 3550 Exibições
- Última mensagem por fernandocez

Sáb Fev 26, 2011 22:29
Geometria Plana
-
- Questão prova concurso
por fernandocez » Sáb Fev 26, 2011 23:27
- 3 Respostas
- 2497 Exibições
- Última mensagem por fernandocez

Dom Fev 27, 2011 10:33
Funções
-
- Questão prova concurso (sen e cos)
por fernandocez » Qua Mar 02, 2011 11:26
- 13 Respostas
- 9264 Exibições
- Última mensagem por fernandocez

Dom Mar 13, 2011 12:18
Trigonometria
-
- Questão prova concurso com Latitude
por fernandocez » Sáb Fev 26, 2011 23:38
- 2 Respostas
- 1820 Exibições
- Última mensagem por fernandocez

Qua Mar 02, 2011 11:27
Geometria Plana
-
- Questão prova concurso combinatória
por fernandocez » Ter Mar 01, 2011 12:35
- 2 Respostas
- 2667 Exibições
- Última mensagem por fernandocez

Qui Mar 03, 2011 22:47
Estatística
Usuários navegando neste fórum: Nenhum usuário registrado e 0 visitantes
Assunto:
Exercicios de polinomios
Autor:
shaft - Qua Jun 30, 2010 17:30

Então, o exercicio pede para encontrar

.
Bom, tentei resolver a questão acima desenvolvendo as duas partes em ( )...Logo dps cheguei em um resultado q nao soube o q fazer mais.
Se vcs puderem ajudar !
Assunto:
Exercicios de polinomios
Autor:
Douglasm - Qua Jun 30, 2010 17:53
Bom, se desenvolvermos isso, encontramos:

Para que os polinômios sejam iguais, seus respectivos coeficientes devem ser iguais (ax = bx ; ax² = bx², etc.):


Somando a primeira e a segunda equação:

Finalmente:

Até a próxima.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
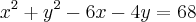 . O maior valor possível de y é:
. O maior valor possível de y é: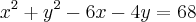


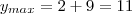 . Se ele pedisse o mínimo, seria o centro menos o raio. Se ele pedisse mais afastado em x, seria o equivalente só que usando coordenadas do x.
. Se ele pedisse o mínimo, seria o centro menos o raio. Se ele pedisse mais afastado em x, seria o equivalente só que usando coordenadas do x.

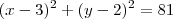 .
.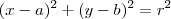

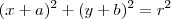 , o centro é
, o centro é ![[x+(-3)]^{2}+[y+(-2)]^{2} = 81 [x+(-3)]^{2}+[y+(-2)]^{2} = 81](/latexrender/pictures/cdd57000c68898d5d4812b31d0d3aab7.png) , teríamos
, teríamos 
 .
.



