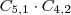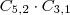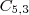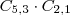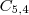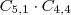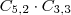por Rejane Sampaio » Sex Set 12, 2008 23:20
por Rejane Sampaio » Sex Set 12, 2008 23:20
Por favor, me ajude com essa questão.
Transpetro- 2006 Em um posto de observação foi montado um sinaleiro de formato pentagonal e em cada um de seus vertices foram colocadas duas lâmpadas de cores distintas, escolhidas entre 5 vermelhas e 5 verdes. Convenciona-se que, para a transmissão de uma mensagem, não pode ser acesa mais do que uma lâmpada por vértice, e que o número mínimo de vértices iluminados deve ser três. Se, cada vez que um conjunto de lâmpadas é aceso, transmite-se uma mensagem, o total de mensagens que podem ser transmitidas por esse sinaleiro é: resp- 192
-
Rejane Sampaio
- Usuário Ativo

-
- Mensagens: 14
- Registrado em: Sex Set 12, 2008 22:25
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Administração
- Andamento: formado
 por admin » Ter Set 16, 2008 20:07
por admin » Ter Set 16, 2008 20:07
Olá
Rejane Sampaio, boas-vindas!
Sugiro dividir em 3 casos: 3 vértices acesos, 4 vértices acesos e 5 vértices acesos.
Lembrando que um vértice aceso significa uma única lâmpada acesa no vértice correspondente.
Para simplificar, considere a seguinte nomeação:
A: vértice com uma lâmpada vermelha acesa;
B: vértice com uma lâmpada verde acesa;
Caso 1) 3 vértices acesos1A e 2B =
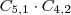
2A e 1B =
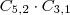
3A =
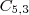
3B =
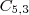 Caso 2) 4 vértices acesos
Caso 2) 4 vértices acesos1A e 3B =

2A e 2B =

3A e 1B =
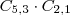
4A =
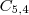
4B =
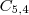 Caso 3) 5 vértices acesos
Caso 3) 5 vértices acesos1A e 4B =
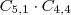
2A e 3B =
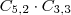
3A e 2B =

4A e 1B =

5A =

5B =

Bons estudos!
-

admin
- Colaborador Administrador - Professor

-
- Mensagens: 885
- Registrado em: Qui Jul 19, 2007 10:58
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Licenciatura em Matemática IME-USP
- Andamento: formado
 por Rejane Sampaio » Qua Set 17, 2008 12:43
por Rejane Sampaio » Qua Set 17, 2008 12:43
muito obrigada Fábio, agora entendi. Mas achei essa questão bem complicada!
-
Rejane Sampaio
- Usuário Ativo

-
- Mensagens: 14
- Registrado em: Sex Set 12, 2008 22:25
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Administração
- Andamento: formado
 por Angela Aguiar » Sex Abr 13, 2012 21:32
por Angela Aguiar » Sex Abr 13, 2012 21:32
Fabiosousa,
Boa noite, tenho uma dúvida na sua resolução.
Quando você cita a combinação envolvendo as lâmpadas verdes "B", você considerou 4 luzes, num universo de 5, e, ainda, foi reduzindo para 3, 2..., ou seja, n=4 e não n=5. O mesmo não aconteceu com a lâmpadass vermelhas "A" , essas você considerou n=5.
Não consegui enxergar no enunciado nada que me indicasse esse passo.
Vou abusar de seu conhecimento e fazer mais uma pergunta. É possível a resolução por meio da permutação circular com repetição? Obrigada
-
Angela Aguiar
- Novo Usuário

-
- Mensagens: 1
- Registrado em: Sex Abr 13, 2012 21:10
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Direito
- Andamento: formado
 por Neilson » Ter Mai 01, 2012 01:23
por Neilson » Ter Mai 01, 2012 01:23
no caso dessa questao, quando estao os 5 vertices acesos, considerando que existam 4 luzes vermelhas acesas, haverá 1 verde acesa (4A e 1B), 3 vermelhas implicarão em 2verdes (3A e 2B) e assim por diante (2A e 3B, 1A e 4B).
quando vc calcula a combinação de se ter uma lampada acesa de uma cor das 5 lampadas possiveis, sobram depois apenas 4 outras lampadas para 4 posições possiveis, não importando a ordem em q elas aparecerão, por isso nao cabe aqui usar permutação circular
espero ter ajudado
-
Neilson
- Novo Usuário

-
- Mensagens: 1
- Registrado em: Ter Mai 01, 2012 00:50
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Matematica
- Andamento: formado
Voltar para Estatística
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- (( Analise combinatória ))
por Roberta » Dom Jul 13, 2008 17:28
- 8 Respostas
- 16355 Exibições
- Última mensagem por Aparecida

Sáb Mai 05, 2012 00:07
Estatística
-
- Análise Combinatória
por Rejane Sampaio » Sex Set 12, 2008 23:26
- 2 Respostas
- 8468 Exibições
- Última mensagem por Rejane Sampaio

Seg Set 15, 2008 10:08
Estatística
-
- Análise Combinatória
por Rejane Sampaio » Qua Set 17, 2008 15:52
- 3 Respostas
- 7921 Exibições
- Última mensagem por Rejane Sampaio

Qui Set 25, 2008 10:43
Estatística
-
- Análise Combinatória
por Rejane Sampaio » Qua Set 17, 2008 15:56
- 2 Respostas
- 6620 Exibições
- Última mensagem por Rejane Sampaio

Seg Set 22, 2008 11:27
Estatística
-
- Análise Combinatória
por Rejane Sampaio » Qua Set 17, 2008 16:04
- 1 Respostas
- 8313 Exibições
- Última mensagem por juliomarcos

Qui Set 18, 2008 13:14
Estatística
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
[calculo] derivada
Autor:
beel - Seg Out 24, 2011 16:59
Para derivar a função
(16-2x)(21-x).x
como é melhor fazer?
derivar primeiro sei la, ((16-2x)(21-x))' achar o resultado (y)
e depois achar (y.x)' ?
Assunto:
[calculo] derivada
Autor:
MarceloFantini - Seg Out 24, 2011 17:15
Você poderia fazer a distributiva e derivar como um polinômio comum.
Assunto:
[calculo] derivada
Autor:
wellersonobelix - Dom Mai 31, 2015 17:26
Funciona da mesma forma que derivada de x.y.z, ou seja, x'.y.z+x.y'.z+x.y.z' substitui cada expressão pelas variáveis e x',y' e z' é derivada de cada um
Assunto:
[calculo] derivada
Autor:
wellersonobelix - Dom Mai 31, 2015 17:31
derivada de (16-2x)=-2
derivada de (21-x)=-1
derivada de x=1
derivada de (16-2x)(21-x)x=-2.(21-x)x+(-1).(16-2x)x +1.(16-2x)(21-x)
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.