Função Exponencial - UnB

[kamillanjb]

(UnB) Em um experimento com uma colônia de bactérias, observou-se que havia 5.000 bactérias vinte minutos após o início do experimento e, dez minutos mais tarde, havia 8.500
bactérias. Suponha que a população da colônia cresce exponencialmente, de acordo com a função P(t) = 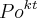, em que Po é a população inicial , k é uma constante positiva e P(t) é a população t minutos após o início do experimento. Calcule o valor de 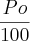, desprezando a parte fracionária de seu resultado, caso exista.

Obs: Bom, meu erro esta sendo nas contas finais. Espero que possam me ajudar. Beijos e desde já agradeço

[Elcioschin]

Parece-me que faltou algo no enunciado:

Qual é a base do expoente kt ? A base é Po ou é um número que não consta no enunciado?

[kamillanjb]

Bom, a questão me foi passada assim. E eu também coloquei a questão no google, e ela se encontra do mesmo modo, sem modificações. =)

[Elcioschin]

kamillanjb

A fórmula padrão para estes casos é:

P = Po*b^k*t onde b é uma base: ´pode ser base 10, base 2, base e, etc.

Sem saber a base fica complicado para resolver.

Você tem o gabarito?