a) o conteudo da lata é ingerido imediatamente.
b) O alccol ingerido entra na corrente sanguinea numa proporção de 20% do que foi consumido.
c) A concentração de alcool em cada lata é de 4% ou 32g/l.
d) a taxa de eliminação é de 0,75% por minuto.
e) um individuo considerado bebado quando a concentração de alcool no sangue é de 2,5g/l.
F) suponha também qua tal individuo tenha cerca de 5 litros de sangue em seu corpo.
G) admita que a concentração alcoolica no sangue do individuo tem decaimento exponencial.Assim sendo C(t)=
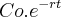 , onde Co = concentração inicial e r = 0,0075(min)^-1
, onde Co = concentração inicial e r = 0,0075(min)^-1Comentário:
O exercicio tem tantos dados que confunde a cabeça da gente,é uma atividade da faculdade e estou com dificuldades .
Acredito que seja melhor calcular lata a lata.
concentração de alccol por lata = 11,2g por lata
considerado bebado com 12,5g de alcool em 5 litros de sangue.


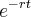



 , avisa que eu resolvo.
, avisa que eu resolvo.

