 por 380625 » Seg Fev 28, 2011 12:54
por 380625 » Seg Fev 28, 2011 12:54
Bom dia estou com muita dificuldades para resolver equações desse tipo:
Se 0<x<pi, as raizes da equação cos^2x - sen ^2( pi - x)=1/2 são:
Obs: o x esta no intervalo o menor igual a x e menor igual a pi.
-
380625
- Usuário Dedicado

-
- Mensagens: 48
- Registrado em: Sex Fev 18, 2011 17:38
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Física
- Andamento: cursando
 por LuizAquino » Seg Fev 28, 2011 18:05
por LuizAquino » Seg Fev 28, 2011 18:05
380625 escreveu:Se
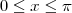
, as raízes da equação
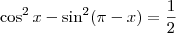
são:
Sabemos que
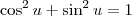
, para qualquer ângulo
u. Portanto, a equação é equivalente a:
![\cos^2x - [1 - \cos ^2(\pi - x)]=\frac{1}{2} \cos^2x - [1 - \cos ^2(\pi - x)]=\frac{1}{2}](/latexrender/pictures/79fd8ff8a24b7e161d25a54d5c4bfc88.png)
Lembrando-se que
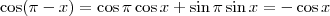
, temos que:
![\cos^2x - [1 - (-\cos x)^2]=\frac{1}{2} \cos^2x - [1 - (-\cos x)^2]=\frac{1}{2}](/latexrender/pictures/6efea19b1c0b8ca487a23805103b4b27.png)
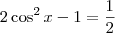
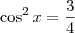
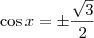
O ângulo do primeiro quadrante que tem cosseno igual a

é

. Já o ângulo do segundo quadrante que tem cosseno igual a
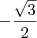
é
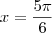
. Portanto, as raízes são
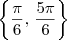
380625 escreveu:estou com muita dificuldades para resolver equações desse tipo
Muito provavelmente essa dificuldade deve-se ao fato de você não conhecer as identidades trigonométricas. Não tem jeito: você tem que estudá-las antes de fazer equações assim.
380625 escreveu:Obs: o x esta no intervalo o menor igual a x e menor igual a pi.
Por favor, faça uso do recurso LaTeX disponível aqui no fórum para digitar os símbolos adequados. Se ainda não estiver bem treinado, você pode usar o botão "Editor de Fórmulas", disponível na edição de suas mensagens.

- botao-editor-de-formulas.png (2.82 KiB) Exibido 699 vezes
-

LuizAquino
- Colaborador Moderador - Professor

-
- Mensagens: 2654
- Registrado em: Sex Jan 21, 2011 09:11
- Localização: Teófilo Otoni - MG
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Mestrado - Modelagem Computacional
- Andamento: formado
-
Voltar para Funções
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Funções reais. como resolver estas funções...
por LEANDRO HENRIQUE » Ter Mar 04, 2014 18:43
- 0 Respostas
- 3429 Exibições
- Última mensagem por LEANDRO HENRIQUE

Ter Mar 04, 2014 18:43
Funções
-
- [Funções] Domínio e a imagem de funções
 por concurseironf » Qui Ago 21, 2014 12:24
por concurseironf » Qui Ago 21, 2014 12:24
- 1 Respostas
- 4201 Exibições
- Última mensagem por Pessoa Estranha

Sex Ago 22, 2014 20:11
Funções
-
- [Funções] questões de funções
por Zandrojr » Qua Ago 31, 2011 11:39
- 0 Respostas
- 3141 Exibições
- Última mensagem por Zandrojr

Qua Ago 31, 2011 11:39
Funções
-
- Funções
por Revelants » Dom Out 05, 2008 15:07
- 1 Respostas
- 3394 Exibições
- Última mensagem por Molina

Dom Out 05, 2008 15:53
Cálculo: Limites, Derivadas e Integrais
-
- Funçoes
por Luna » Seg Set 28, 2009 20:02
- 1 Respostas
- 2999 Exibições
- Última mensagem por Marcampucio

Seg Set 28, 2009 21:35
Funções
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
[Função] do primeiro grau e quadratica
Autor:
Thassya - Sáb Out 01, 2011 16:20
1) Para que os pontos (1,3) e (-3,1) pertençam ao grafico da função f(X)=ax + b ,o valor de b-a deve ser ?
2)Qual o maior valor assumido pela função f : [-7 ,10] em R definida por f(x) = x ao quadrado - 5x + 9?
3) A função f, do primeiro grau, é definida pos f(x)= 3x + k para que o gráfico de f corte o eixo das ordenadas no ponto de ordenada 5 é?
Assunto:
[Função] do primeiro grau e quadratica
Autor:
Neperiano - Sáb Out 01, 2011 19:46
Ola
Qual as suas dúvidas?
O que você não está conseguindo fazer?
Nos mostre para podermos ajudar
Atenciosamente
Assunto:
[Função] do primeiro grau e quadratica
Autor:
joaofonseca - Sáb Out 01, 2011 20:15
1)Dados dois pontos A=(1,3) e B=(-3,1) de uma reta, é possivel definir a sua equação.


Em

substitui-se
m, substitui-se
y e
x por um dos pares ordenados, e resolve-se em ordem a
b.

2)Na equação

não existem zeros.Senão vejamos
Completando o quadrado,

As coordenadas do vertice da parabola são

O eixo de simetria é a reta

.Como se pode observar o vertice está acima do eixo Ox, estando parabola virada para cima, o vertice é um mínimo absoluto.Então basta calcular a função para os valores dos extremos do intervalo.
f(-7)=93
f(10)=59
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.



, as raízes da equação
são:
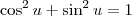 , para qualquer ângulo u. Portanto, a equação é equivalente a:
, para qualquer ângulo u. Portanto, a equação é equivalente a:![\cos^2x - [1 - \cos ^2(\pi - x)]=\frac{1}{2} \cos^2x - [1 - \cos ^2(\pi - x)]=\frac{1}{2}](/latexrender/pictures/79fd8ff8a24b7e161d25a54d5c4bfc88.png)
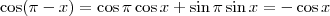 , temos que:
, temos que: ![\cos^2x - [1 - (-\cos x)^2]=\frac{1}{2} \cos^2x - [1 - (-\cos x)^2]=\frac{1}{2}](/latexrender/pictures/6efea19b1c0b8ca487a23805103b4b27.png)
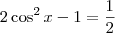
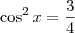
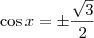
 é
é  . Já o ângulo do segundo quadrante que tem cosseno igual a
. Já o ângulo do segundo quadrante que tem cosseno igual a 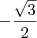 é
é 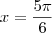 . Portanto, as raízes são
. Portanto, as raízes são 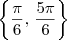



 substitui-se m, substitui-se y e x por um dos pares ordenados, e resolve-se em ordem a b.
substitui-se m, substitui-se y e x por um dos pares ordenados, e resolve-se em ordem a b.
 não existem zeros.Senão vejamos
não existem zeros.Senão vejamos

 .Como se pode observar o vertice está acima do eixo Ox, estando parabola virada para cima, o vertice é um mínimo absoluto.Então basta calcular a função para os valores dos extremos do intervalo.
.Como se pode observar o vertice está acima do eixo Ox, estando parabola virada para cima, o vertice é um mínimo absoluto.Então basta calcular a função para os valores dos extremos do intervalo.