Prezados, boa noite!
Estou tentando resolver uma questão de sistemas de coordenadas esfericas, tentando achar os lados e o volume.
Existem tres arestas a serem encontradas so que encontrei so uma o dr que alias é netido. Agora os outros como rsenothetadphi e rdtheta não consegui enxergar como foi encontrado esse expressão! tentei alguma coisa pelo triangulo retangulo, mas não tenho certeza se estar certo!
Segue em anexo a figura com os lados a serem encontrados
Obrigada desde já!


 (em radianos) e raio
(em radianos) e raio  .
.
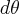 é =
é =  tem medida igual a
tem medida igual a  .
.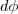 e raio
e raio 
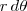
![\frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}} \frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}}](/latexrender/pictures/981987c7bcdf9f8f498ca4605785636a.png)
![\sqrt[]{2} \sqrt[]{2}](/latexrender/pictures/f21662d1cabab6e8b273a4b6f1cd663a.png)
 e elevar ao quadrado os dois lados)
e elevar ao quadrado os dois lados)