 por feraferrari » Qui Fev 24, 2011 15:12
por feraferrari » Qui Fev 24, 2011 15:12
Boa taarde. Estou com duvidas para resolver essa. Não consigo simbolizar essas proposiçoes com esse esquema de simbolização
p : 1 é par.
q : 2 é par.
e conectivos dentre ~, ^, v, ->
(a) Ao menos um dos numeros 1 ou 2 é par.
(b) No maximo um dos numeros 1 ou 2 é par.
(c) Exatamente um dos numeros 1 ou 2 é par.
-
feraferrari
- Novo Usuário

-
- Mensagens: 2
- Registrado em: Qui Fev 24, 2011 13:42
- Formação Escolar: ENSINO MÉDIO
- Área/Curso: licenciatura matematica
- Andamento: cursando
 por LuizAquino » Qui Fev 24, 2011 16:29
por LuizAquino » Qui Fev 24, 2011 16:29
feraferrari escreveu:p : 1 é par.
q : 2 é par.
e conectivos dentre ~, ^, v, ->
(a) Ao menos um dos numeros 1 ou 2 é par.
(b) No maximo um dos numeros 1 ou 2 é par.
(c) Exatamente um dos numeros 1 ou 2 é par.
Vou tentar lhe ajudar construindo a tabela verdade para essas situações (considere que "ser par" significa V):
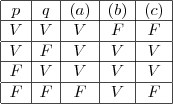
E agora, consegue perceber que conectivos usar?
-

LuizAquino
- Colaborador Moderador - Professor

-
- Mensagens: 2654
- Registrado em: Sex Jan 21, 2011 09:11
- Localização: Teófilo Otoni - MG
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Mestrado - Modelagem Computacional
- Andamento: formado
-
 por feraferrari » Sex Fev 25, 2011 00:21
por feraferrari » Sex Fev 25, 2011 00:21
Obrigado professor! consegui fechar a questão.
-
feraferrari
- Novo Usuário

-
- Mensagens: 2
- Registrado em: Qui Fev 24, 2011 13:42
- Formação Escolar: ENSINO MÉDIO
- Área/Curso: licenciatura matematica
- Andamento: cursando
 por LuizAquino » Sex Fev 25, 2011 08:54
por LuizAquino » Sex Fev 25, 2011 08:54
Para que outros também possam aprender com esse exercício, segue a solução.
(a) Disjunção:
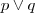
(b) Negação da Conjunção:
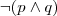
(c) Disjunção Exclusiva:
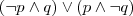
-

LuizAquino
- Colaborador Moderador - Professor

-
- Mensagens: 2654
- Registrado em: Sex Jan 21, 2011 09:11
- Localização: Teófilo Otoni - MG
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Mestrado - Modelagem Computacional
- Andamento: formado
-
Voltar para Funções
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Proposições com variáveis
por rrt » Dom Jul 28, 2013 20:57
- 5 Respostas
- 3394 Exibições
- Última mensagem por rrt

Seg Jul 29, 2013 18:32
Funções
-
- considere as proposiçoes
por flavio neves » Qua Fev 24, 2016 15:10
- 0 Respostas
- 1358 Exibições
- Última mensagem por flavio neves

Qua Fev 24, 2016 15:10
Lógica
-
- Negação das proposições
 por roninhasmr » Seg Nov 13, 2017 14:30
por roninhasmr » Seg Nov 13, 2017 14:30
- 0 Respostas
- 1956 Exibições
- Última mensagem por roninhasmr

Seg Nov 13, 2017 14:30
Lógica
-
- proposições lógicas -torneio
por adrianosaldanha » Qui Out 20, 2011 17:06
- 1 Respostas
- 1818 Exibições
- Última mensagem por fraol

Qua Dez 21, 2011 00:00
Sequências
-
- sistema de proposiçoes e conectivos
por flavio neves » Ter Fev 23, 2016 20:16
- 0 Respostas
- 2405 Exibições
- Última mensagem por flavio neves

Ter Fev 23, 2016 20:16
Lógica
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
Simplifique a expressão com radicais duplos
Autor:
Balanar - Seg Ago 09, 2010 04:01
Simplifique a expressão com radicais duplos abaixo:
![\frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}} \frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}}](/latexrender/pictures/981987c7bcdf9f8f498ca4605785636a.png)
Resposta:
Dica:
![\sqrt[]{2} \sqrt[]{2}](/latexrender/pictures/f21662d1cabab6e8b273a4b6f1cd663a.png)
(dica : igualar a expressão a

e elevar ao quadrado os dois lados)
Assunto:
Simplifique a expressão com radicais duplos
Autor:
MarceloFantini - Qua Ago 11, 2010 05:46
É só fazer a dica.
Assunto:
Simplifique a expressão com radicais duplos
Autor:
Soprano - Sex Mar 04, 2016 09:49
Olá,
O resultado é igual a 1, certo?
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.


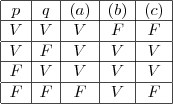

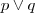
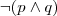
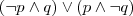
![\frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}} \frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}}](/latexrender/pictures/981987c7bcdf9f8f498ca4605785636a.png)
![\sqrt[]{2} \sqrt[]{2}](/latexrender/pictures/f21662d1cabab6e8b273a4b6f1cd663a.png)
 e elevar ao quadrado os dois lados)
e elevar ao quadrado os dois lados)