 por baianinha » Seg Fev 21, 2011 12:59
por baianinha » Seg Fev 21, 2011 12:59
-
baianinha
- Usuário Ativo

-
- Mensagens: 23
- Registrado em: Qui Dez 16, 2010 12:15
- Formação Escolar: ENSINO MÉDIO PROFISSIONALIZANTE
- Área/Curso: matematica
- Andamento: cursando
 por LuizAquino » Ter Fev 22, 2011 16:44
por LuizAquino » Ter Fev 22, 2011 16:44
baianinha escreveu:Sabe-se que a matriz de uma transformação linear

é dada por
![[T]_A^B = \begin{bmatrix} 1 & 1 & 0 \\ 0 & 1 & 0 \\ 0 & 0 & -1 \\ 0 & 0 & 1 \end{bmatrix} [T]_A^B = \begin{bmatrix} 1 & 1 & 0 \\ 0 & 1 & 0 \\ 0 & 0 & -1 \\ 0 & 0 & 1 \end{bmatrix}](/latexrender/pictures/47c2b8e373a3cbbcb8866e0340699d7f.png)
,
considerando as bases
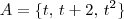
de
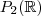
e
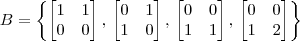
de
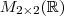
.
Encontrar a expressão de T(p).
Do conhecimento de Álgebra Linear, sabemos que:
![[T(p)]_B = [T]_A^B[p]_A [T(p)]_B = [T]_A^B[p]_A](/latexrender/pictures/3a93f5d0d1f92a231aa44c06f4ed5684.png)
onde
![[T(p)]_B [T(p)]_B](/latexrender/pictures/0623fe724e2938dcf2045ddec7cd0665.png)
- vetor de coordenadas de T(p) na base B;
![[T]_A^B [T]_A^B](/latexrender/pictures/f6e319aa809880a0d493de6315e37e04.png)
- matriz de T em relação as bases A e B;
![[p]_A [p]_A](/latexrender/pictures/f19f70d560dcff52eeac3ddc1baf38e0.png)
- vetor de coordenadas de p na base A;
Primeiro, vamos determinar quem é o vetor de coordenadas de p na base A. Sabemos que um polinômio de 2° grau é dado por
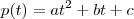
. Nós queremos descobrir os escalares k1, k2 e k3 de modo que
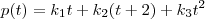
. Arrumando essa equação e comparando os coeficientes dos polinômios, é fácil obter que
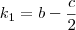
,
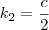
,

. Portanto, temos que:
![[p]_A = \begin{bmatrix} b -\frac{c}{2} \\ \frac{c}{2} \\ a \end{bmatrix}_A [p]_A = \begin{bmatrix} b -\frac{c}{2} \\ \frac{c}{2} \\ a \end{bmatrix}_A](/latexrender/pictures/f45165aaa3dcd73405a55ee2c811ac2e.png)
Desse modo, obtemos que:
![[T(p)]_B = [T]_A^B[p]_A = \begin{bmatrix} 1 & 1 & 0 \\ 0 & 1 & 0 \\ 0 & 0 & -1 \\ 0 & 0 & 1 \end{bmatrix}_A^B \begin{bmatrix} b -\frac{c}{2} \\ \frac{c}{2} \\ a \end{bmatrix}_A = \begin{bmatrix} b \\ \frac{c}{2} \\ - a \\ a \end{bmatrix}_B [T(p)]_B = [T]_A^B[p]_A = \begin{bmatrix} 1 & 1 & 0 \\ 0 & 1 & 0 \\ 0 & 0 & -1 \\ 0 & 0 & 1 \end{bmatrix}_A^B \begin{bmatrix} b -\frac{c}{2} \\ \frac{c}{2} \\ a \end{bmatrix}_A = \begin{bmatrix} b \\ \frac{c}{2} \\ - a \\ a \end{bmatrix}_B](/latexrender/pictures/9505de078f9f7005965576b081c636d1.png)
Escrevendo
![[T(p)]_B [T(p)]_B](/latexrender/pictures/0623fe724e2938dcf2045ddec7cd0665.png)
usando o vetor de coordenadas calculado e a base B dada, nós temos:
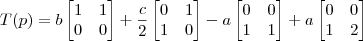
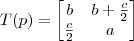
-

LuizAquino
- Colaborador Moderador - Professor

-
- Mensagens: 2654
- Registrado em: Sex Jan 21, 2011 09:11
- Localização: Teófilo Otoni - MG
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Mestrado - Modelagem Computacional
- Andamento: formado
-
Voltar para Álgebra Linear
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- [Algebra Linear] - Matriz de uma trasnformacao linear, Ajuda
por rodrigojuara » Dom Nov 30, 2014 15:05
- 1 Respostas
- 8150 Exibições
- Última mensagem por adauto martins

Seg Dez 01, 2014 16:12
Álgebra Linear
-
- [Algebra Linear] - Composição de transformação Linear
por aligames321 » Ter Dez 04, 2012 23:53
- 1 Respostas
- 10524 Exibições
- Última mensagem por young_jedi

Qua Dez 05, 2012 12:45
Álgebra Linear
-
- Álgebra Linear -Transformação linear- Isomorfismo
por anapaulasql » Ter Jan 27, 2015 22:08
- 1 Respostas
- 11556 Exibições
- Última mensagem por adauto martins

Ter Mar 29, 2016 13:15
Álgebra Linear
-
- [Álgebra Linear] Transformação Linear Idenpotente
por Zubumafu67 » Ter Nov 17, 2020 11:38
- 0 Respostas
- 13597 Exibições
- Última mensagem por Zubumafu67

Ter Nov 17, 2020 11:38
Álgebra Linear
-
- [Álgebra Linear] Transformação linear
por Debby » Dom Mai 27, 2012 12:17
- 2 Respostas
- 9134 Exibições
- Última mensagem por Debby

Dom Mai 27, 2012 20:27
Álgebra Linear
Usuários navegando neste fórum: Nenhum usuário registrado e 0 visitantes
Assunto:
[Função] do primeiro grau e quadratica
Autor:
Thassya - Sáb Out 01, 2011 16:20
1) Para que os pontos (1,3) e (-3,1) pertençam ao grafico da função f(X)=ax + b ,o valor de b-a deve ser ?
2)Qual o maior valor assumido pela função f : [-7 ,10] em R definida por f(x) = x ao quadrado - 5x + 9?
3) A função f, do primeiro grau, é definida pos f(x)= 3x + k para que o gráfico de f corte o eixo das ordenadas no ponto de ordenada 5 é?
Assunto:
[Função] do primeiro grau e quadratica
Autor:
Neperiano - Sáb Out 01, 2011 19:46
Ola
Qual as suas dúvidas?
O que você não está conseguindo fazer?
Nos mostre para podermos ajudar
Atenciosamente
Assunto:
[Função] do primeiro grau e quadratica
Autor:
joaofonseca - Sáb Out 01, 2011 20:15
1)Dados dois pontos A=(1,3) e B=(-3,1) de uma reta, é possivel definir a sua equação.


Em

substitui-se
m, substitui-se
y e
x por um dos pares ordenados, e resolve-se em ordem a
b.

2)Na equação

não existem zeros.Senão vejamos
Completando o quadrado,

As coordenadas do vertice da parabola são

O eixo de simetria é a reta

.Como se pode observar o vertice está acima do eixo Ox, estando parabola virada para cima, o vertice é um mínimo absoluto.Então basta calcular a função para os valores dos extremos do intervalo.
f(-7)=93
f(10)=59
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
 (R)
(R)
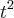 } do
} do 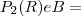
![{\left[
\begin{vmatrix}
1 & 1 \\
0 & 0
\end{vmatrix}
\right], {\left[
\begin{vmatrix}
1 & 1 \\
0 & 0
\end{vmatrix}
\right],](/latexrender/pictures/30224cef379713444b07169de3eb7b7d.png)
![\left[
\begin{vmatrix}
0 & 1 \\
1 & 0
\end{vmatrix}
\right], \left[
\begin{vmatrix}
0 & 1 \\
1 & 0
\end{vmatrix}
\right],](/latexrender/pictures/892179d9a47cb9a55b6029426629014c.png)
![\left[
\begin{vmatrix}
0 & 0 \\
1 & 1
\end{vmatrix},}
\right], \left[
\begin{vmatrix}
0 & 0 \\
1 & 1
\end{vmatrix},}
\right],](/latexrender/pictures/6bca50fb8ca4c49f3f8141ac14ce9e85.png)
![\left[
\begin{vmatrix}
0 & 0 \\
1 & 2
\end{vmatrix}
\right], \left[
\begin{vmatrix}
0 & 0 \\
1 & 2
\end{vmatrix}
\right],](/latexrender/pictures/4c4c1bb8edd9cefd669f6d47f9527794.png)
![\left[T \right]A.B=
\begin{pmatrix}
1 & 1 & 0 \\
0 & 1 & 0 \\
0 & 0 & -1 \\
0 & 0 & 1
\end{pmatrix} \left[T \right]A.B=
\begin{pmatrix}
1 & 1 & 0 \\
0 & 1 & 0 \\
0 & 0 & -1 \\
0 & 0 & 1
\end{pmatrix}](/latexrender/pictures/4caa26fdd7e878bc859bc617ed953119.png)

 (R)
(R)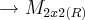
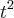 } do
} do 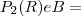
![{\left[
\begin{vmatrix}
1 & 1 \\
0 & 0
\end{vmatrix}
\right], {\left[
\begin{vmatrix}
1 & 1 \\
0 & 0
\end{vmatrix}
\right],](/latexrender/pictures/30224cef379713444b07169de3eb7b7d.png)
![\left[
\begin{vmatrix}
0 & 1 \\
1 & 0
\end{vmatrix}
\right], \left[
\begin{vmatrix}
0 & 1 \\
1 & 0
\end{vmatrix}
\right],](/latexrender/pictures/892179d9a47cb9a55b6029426629014c.png)
![\left[
\begin{vmatrix}
0 & 0 \\
1 & 1
\end{vmatrix},}
\right], \left[
\begin{vmatrix}
0 & 0 \\
1 & 1
\end{vmatrix},}
\right],](/latexrender/pictures/6bca50fb8ca4c49f3f8141ac14ce9e85.png)
![\left[
\begin{vmatrix}
0 & 0 \\
1 & 2
\end{vmatrix}
\right], \left[
\begin{vmatrix}
0 & 0 \\
1 & 2
\end{vmatrix}
\right],](/latexrender/pictures/4c4c1bb8edd9cefd669f6d47f9527794.png)
![\left[T \right]A.B=
\begin{pmatrix}
1 & 1 & 0 \\
0 & 1 & 0 \\
0 & 0 & -1 \\
0 & 0 & 1
\end{pmatrix} \left[T \right]A.B=
\begin{pmatrix}
1 & 1 & 0 \\
0 & 1 & 0 \\
0 & 0 & -1 \\
0 & 0 & 1
\end{pmatrix}](/latexrender/pictures/4caa26fdd7e878bc859bc617ed953119.png)

,
de
e
de
.
![[T(p)]_B = [T]_A^B[p]_A [T(p)]_B = [T]_A^B[p]_A](/latexrender/pictures/3a93f5d0d1f92a231aa44c06f4ed5684.png)
![[T(p)]_B [T(p)]_B](/latexrender/pictures/0623fe724e2938dcf2045ddec7cd0665.png) - vetor de coordenadas de T(p) na base B;
- vetor de coordenadas de T(p) na base B;![[T]_A^B [T]_A^B](/latexrender/pictures/f6e319aa809880a0d493de6315e37e04.png) - matriz de T em relação as bases A e B;
- matriz de T em relação as bases A e B;![[p]_A [p]_A](/latexrender/pictures/f19f70d560dcff52eeac3ddc1baf38e0.png) - vetor de coordenadas de p na base A;
- vetor de coordenadas de p na base A;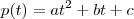 . Nós queremos descobrir os escalares k1, k2 e k3 de modo que
. Nós queremos descobrir os escalares k1, k2 e k3 de modo que 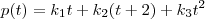 . Arrumando essa equação e comparando os coeficientes dos polinômios, é fácil obter que
. Arrumando essa equação e comparando os coeficientes dos polinômios, é fácil obter que 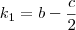 ,
, 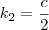 ,
,  . Portanto, temos que:
. Portanto, temos que:![[p]_A = \begin{bmatrix} b -\frac{c}{2} \\ \frac{c}{2} \\ a \end{bmatrix}_A [p]_A = \begin{bmatrix} b -\frac{c}{2} \\ \frac{c}{2} \\ a \end{bmatrix}_A](/latexrender/pictures/f45165aaa3dcd73405a55ee2c811ac2e.png)
![[T(p)]_B = [T]_A^B[p]_A = \begin{bmatrix} 1 & 1 & 0 \\ 0 & 1 & 0 \\ 0 & 0 & -1 \\ 0 & 0 & 1 \end{bmatrix}_A^B \begin{bmatrix} b -\frac{c}{2} \\ \frac{c}{2} \\ a \end{bmatrix}_A = \begin{bmatrix} b \\ \frac{c}{2} \\ - a \\ a \end{bmatrix}_B [T(p)]_B = [T]_A^B[p]_A = \begin{bmatrix} 1 & 1 & 0 \\ 0 & 1 & 0 \\ 0 & 0 & -1 \\ 0 & 0 & 1 \end{bmatrix}_A^B \begin{bmatrix} b -\frac{c}{2} \\ \frac{c}{2} \\ a \end{bmatrix}_A = \begin{bmatrix} b \\ \frac{c}{2} \\ - a \\ a \end{bmatrix}_B](/latexrender/pictures/9505de078f9f7005965576b081c636d1.png)
![[T(p)]_B [T(p)]_B](/latexrender/pictures/0623fe724e2938dcf2045ddec7cd0665.png) usando o vetor de coordenadas calculado e a base B dada, nós temos:
usando o vetor de coordenadas calculado e a base B dada, nós temos: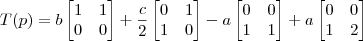
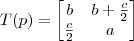



 substitui-se m, substitui-se y e x por um dos pares ordenados, e resolve-se em ordem a b.
substitui-se m, substitui-se y e x por um dos pares ordenados, e resolve-se em ordem a b.
 não existem zeros.Senão vejamos
não existem zeros.Senão vejamos

 .Como se pode observar o vertice está acima do eixo Ox, estando parabola virada para cima, o vertice é um mínimo absoluto.Então basta calcular a função para os valores dos extremos do intervalo.
.Como se pode observar o vertice está acima do eixo Ox, estando parabola virada para cima, o vertice é um mínimo absoluto.Então basta calcular a função para os valores dos extremos do intervalo.