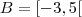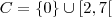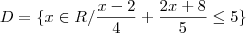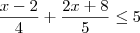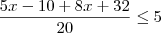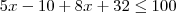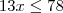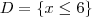por Juliane » Dom Fev 20, 2011 20:31
por Juliane » Dom Fev 20, 2011 20:31
Se
A = { x

N / k < x
<![\sqrt[]{5} \sqrt[]{5}](/latexrender/pictures/0be1c4ad0f7708e4012e708b953ffd6c.png)
} onde k é a solução
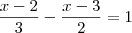
,
B = [m,n[, onde m e n são raízes da equação x² - 2x – 15= 0,
C = {0}

[2,7[ e
D = {x

R/
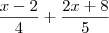 <
< 5}
Determine (D - ?)

(C

B)
Eu encontrei:
A = ]-1, 2]
B = [-5,3[
C = {0,2,3,4,5,6}
D = ]-
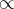
, 6]
-
Juliane
- Usuário Ativo

-
- Mensagens: 12
- Registrado em: Sáb Set 04, 2010 17:29
- Formação Escolar: ENSINO MÉDIO PROFISSIONALIZANTE
- Área/Curso: Edificações
- Andamento: cursando
 por Molina » Seg Fev 21, 2011 16:05
por Molina » Seg Fev 21, 2011 16:05
Boa tarde, Juliane.
Sua dúvida é referente aos conjuntos A, B, C e D ou as operações entre eles?
Vou mostrar a cara destes conjuntos que eu citei acima e caso você tenha dúvida em como opera-los, avise, ok?
Procure além de colocar a questão informar também onde estão suas maiores dificuldades e até mesmo o que você tentou fazer. Isso facilita quem quer te ajudar. Mas vamos lá:
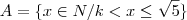
onde
k é a solução
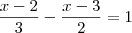
Resolvendo a equação para encontrar o valor de
k:
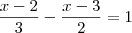
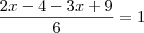
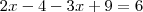
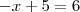

Como os valores de

são naturais maiores do que -1 e menores do que raiz de 5, temos que:
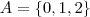 Obs.: Há divergências quanto ao ZERO pertencer ou não aos números naturais. Eu considerei ele natural, mas você precisa ver como seu professor definiu a vocês.
Obs.: Há divergências quanto ao ZERO pertencer ou não aos números naturais. Eu considerei ele natural, mas você precisa ver como seu professor definiu a vocês.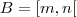
, onde
m e
n são raízes da equação

Resolvendo a equação temos que as raízes são -3 e 5.
Assim:
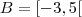
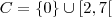
Não há o que fazer. O conjunto está pronto.
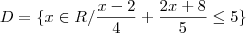
Resolvendo a inequação, temos:
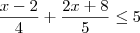
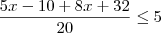
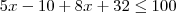
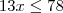

Logo:
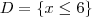
Agora que você já tem os conjuntos, basta fazer a operação entre eles.
Qualquer coisa, informe.
Diego Molina |
CV |
FB |
.COMEquipe AjudaMatemática.com"Existem 10 tipos de pessoas: as que conhecem o sistema binário e as que não conhecem."
-

Molina
- Colaborador Moderador - Professor

-
- Mensagens: 1551
- Registrado em: Dom Jun 01, 2008 14:10
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Licenciatura em Matemática - UFSC
- Andamento: formado
 por Juliane » Ter Fev 22, 2011 09:10
por Juliane » Ter Fev 22, 2011 09:10
Na verdade a minha dúvida era referente a operação entre eles, inclusive eu já havia colocado os elementos dos conjuntos que consegui encontrar...
mas obrigada, eu identifiquei o meu erro, foi no conjunto B
-
Juliane
- Usuário Ativo

-
- Mensagens: 12
- Registrado em: Sáb Set 04, 2010 17:29
- Formação Escolar: ENSINO MÉDIO PROFISSIONALIZANTE
- Área/Curso: Edificações
- Andamento: cursando
Voltar para Álgebra Elementar
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- [Conjuntos] Confusão em teoria dos conjuntos numa questão.
 por Debora Bruna » Seg Jan 11, 2016 17:44
por Debora Bruna » Seg Jan 11, 2016 17:44
- 1 Respostas
- 8838 Exibições
- Última mensagem por DanielFerreira

Sáb Jan 23, 2016 16:44
Conjuntos
-
- [Conjuntos] Dúvida sobre conjuntos vazios
por ALPC » Qui Set 18, 2014 18:28
- 5 Respostas
- 6409 Exibições
- Última mensagem por adauto martins

Seg Set 22, 2014 15:44
Conjuntos
-
- [conjuntos]numeros racionais e conjuntos
por fenixxx » Ter Fev 28, 2012 21:35
- 3 Respostas
- 4724 Exibições
- Última mensagem por DanielFerreira

Sex Mar 02, 2012 00:04
Álgebra Elementar
-
- [Conjuntos] Problema de conjuntos com porcentagem
por Tibes » Qui Jan 31, 2013 14:29
- 1 Respostas
- 7954 Exibições
- Última mensagem por young_jedi

Sex Fev 01, 2013 12:39
Conjuntos
-
- [Conjuntos] Conjuntos e geometria plana
por bencz » Dom Mar 03, 2013 12:58
- 3 Respostas
- 11198 Exibições
- Última mensagem por maison_souza

Sex Nov 14, 2014 13:15
Álgebra Elementar
Usuários navegando neste fórum: Nenhum usuário registrado e 0 visitantes
Assunto:
Taxa de variação
Autor:
felipe_ad - Ter Jun 29, 2010 19:44
Como resolvo uma questao desse tipo:
Uma usina de britagem produz pó de pedra, que ao ser depositado no solo, forma uma pilha cônica onde a altura é aproximadamente igual a 4/3 do raio da base.
(a) Determinar a razão de variação do volume em relação ao raio da base.
(b) Se o raio da base varia a uma taxa de 20 cm/s, qual a razão de variação do volume quando o raio mede 2 m?
A letra (a) consegui resolver e cheguei no resultado correto de

Porem, nao consegui chegar a um resultado correto na letra (b). A resposta certa é

Alguem me ajuda? Agradeço desde já.
Assunto:
Taxa de variação
Autor:
Elcioschin - Qua Jun 30, 2010 20:47
V = (1/3)*pi*r²*h ----> h = 4r/3
V = (1/3)*pi*r²*(4r/3) ----> V = (4*pi/9)*r³
Derivando:
dV/dr = (4*pi/9)*(3r²) -----> dV/dr = 4pi*r²/3
Para dr = 20 cm/s = 0,2 m/s e R = 2 m ----> dV/0,2 = (4*pi*2²)/3 ----> dV = (3,2/3)*pi ----> dV ~= 1,066*pi m³/s
Assunto:
Taxa de variação
Autor:
Guill - Ter Fev 21, 2012 21:17
Temos que o volume é dado por:

Temos, portanto, o volume em função do raio. Podemos diferenciar implicitamente ambos os lados da equação em função do tempo, para encontrar as derivadas em função do tempo:

Sabendo que a taxa de variação do raio é 0,2 m/s e que queremos ataxa de variação do volume quando o raio for 2 m:


Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
 N / k < x <
N / k < x <![\sqrt[]{5} \sqrt[]{5}](/latexrender/pictures/0be1c4ad0f7708e4012e708b953ffd6c.png) } onde k é a solução
} onde k é a solução 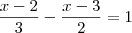 , B = [m,n[, onde m e n são raízes da equação x² - 2x – 15= 0, C = {0}
, B = [m,n[, onde m e n são raízes da equação x² - 2x – 15= 0, C = {0}  [2,7[ e D = {x
[2,7[ e D = {x  R/
R/ 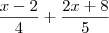 < 5}
< 5} (C
(C  B)
B)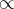 , 6]
, 6]
 N / k < x <
N / k < x <![\sqrt[]{5} \sqrt[]{5}](/latexrender/pictures/0be1c4ad0f7708e4012e708b953ffd6c.png) } onde k é a solução
} onde k é a solução 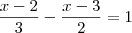 , B = [m,n[, onde m e n são raízes da equação x² - 2x – 15= 0, C = {0}
, B = [m,n[, onde m e n são raízes da equação x² - 2x – 15= 0, C = {0}  [2,7[ e D = {x
[2,7[ e D = {x  R/
R/ 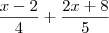 < 5}
< 5} (C
(C  B)
B)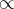 , 6]
, 6]
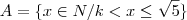 onde k é a solução
onde k é a solução 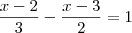
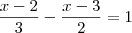
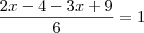
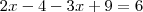
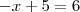

 são naturais maiores do que -1 e menores do que raiz de 5, temos que:
são naturais maiores do que -1 e menores do que raiz de 5, temos que: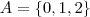
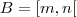 , onde m e n são raízes da equação
, onde m e n são raízes da equação