R= {(x,y)
 IR tal que 0
IR tal que 0  x
x 
 y
y  cox
cox  }: o eixo é 0y
}: o eixo é 0yAguardo ajuda.

 IR tal que 0
IR tal que 0  x
x 
 y
y  cox
cox  }: o eixo é 0y
}: o eixo é 0y
Manoella escreveu:Como faço para encontrar o volume de revolução da região R em torno do eixo indicado:: o eixo é 0y
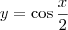 , então
, então 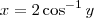 (onde
(onde 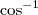 representa a função inversa do cosseno, isto é, o arco-cosseno). Portanto, a área de cada seção transversal será dada por
representa a função inversa do cosseno, isto é, o arco-cosseno). Portanto, a área de cada seção transversal será dada por 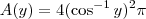 .
.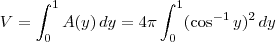
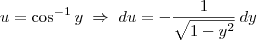
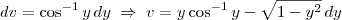
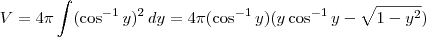
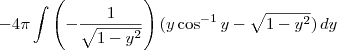
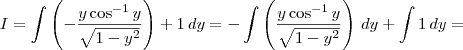
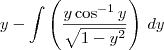
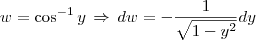
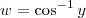 , então
, então 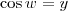 .
.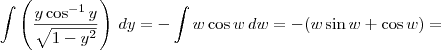
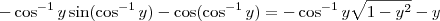
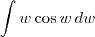 por partes. Além disso, lembre-se que
por partes. Além disso, lembre-se que ![\sin (\cos^{-1}y) = \sqrt{1- [\cos(\cos^{-1} y)]^2} = \sqrt{1- y^2} \sin (\cos^{-1}y) = \sqrt{1- [\cos(\cos^{-1} y)]^2} = \sqrt{1- y^2}](/latexrender/pictures/87c1dba1dab3d8367cb4c8ec3824c295.png) .
.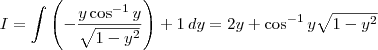
![V = 4\pi\int_0^1 (\cos^{-1} y)^2 \,dy = 4\pi\left[(\cos^{-1} y)\left(y\cos^{-1}y - \sqrt{1-y^2}\right) - 2y - \cos^{-1}y\sqrt{1-y^2}\right]_0^1 V = 4\pi\int_0^1 (\cos^{-1} y)^2 \,dy = 4\pi\left[(\cos^{-1} y)\left(y\cos^{-1}y - \sqrt{1-y^2}\right) - 2y - \cos^{-1}y\sqrt{1-y^2}\right]_0^1](/latexrender/pictures/45f13692c77af165a1777defc8c1a84e.png)
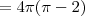 .
.
Voltar para Cálculo: Limites, Derivadas e Integrais
Usuários navegando neste fórum: Nenhum usuário registrado e 5 visitantes
leandro moraes escreveu:pessoal já achei a resposta. o meu erro foi bobo rsrsrrs errei em uma continha de multiplicação, é mole rsrsrsr mas felizmente consegui.