 por lucas7 » Seg Fev 21, 2011 18:09
por lucas7 » Seg Fev 21, 2011 18:09
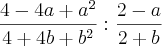
=
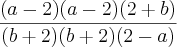
=
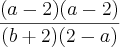
(meu desenvolvimento)
O gabarito diz
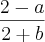
Fiquei na duvida na hora de simplificar para chegar ao resultado do gabarito. Se eu multiplicar
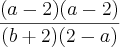
por -1, multiplicaria só o primeiro parênteses do numerado e do denominador, ficando:

, corta o primeiro parentêses do numerador com o segundo parênteses do denominador, ficando

ou
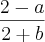
.
Esse meu procedimento está correto?
O gênio, esse poder que deslumbra os olhos humanos, não é outra coisa senão a perseverança bem disfarçada.
Johann Goethe
-
lucas7
- Usuário Parceiro

-
- Mensagens: 53
- Registrado em: Ter Fev 15, 2011 19:43
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia de Controle e Automação
- Andamento: cursando
 por Molina » Seg Fev 21, 2011 19:08
por Molina » Seg Fev 21, 2011 19:08
Diego Molina |
CV |
FB |
.COMEquipe AjudaMatemática.com"Existem 10 tipos de pessoas: as que conhecem o sistema binário e as que não conhecem."
-

Molina
- Colaborador Moderador - Professor

-
- Mensagens: 1551
- Registrado em: Dom Jun 01, 2008 14:10
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Licenciatura em Matemática - UFSC
- Andamento: formado
 por Molina » Seg Fev 21, 2011 22:06
por Molina » Seg Fev 21, 2011 22:06
Olá.
lucas7 escreveu:Entendi. Fiz a experiência e deu certo. Multiplicar a soma por -1 ou um dos parentêses da multiplicação dessa soma fatorada dá no mesmo. Obrigado, molina.
e espero que não haja um limite de perguntas por usuário, porque eu tenho mais uma pergunta:
Não há limite de perguntas por usuários, quanto a isso pode ficar a vontade em postar quantas dúvidas você tiver. Única coisa que pedimos é que seja criado um novo tópico para novas questões, ok? Ou seja, como você tinha uma dúvida de outra questão o certo seria você criar um novo tópico. Isso ajuda o fórum a ficar mais organizado.
Fiz este favorzinho para você e seu tópico foi parar aqui:
viewtopic.php?f=106&t=3857Qualquer dúvida me procure!

Diego Molina |
CV |
FB |
.COMEquipe AjudaMatemática.com"Existem 10 tipos de pessoas: as que conhecem o sistema binário e as que não conhecem."
-

Molina
- Colaborador Moderador - Professor

-
- Mensagens: 1551
- Registrado em: Dom Jun 01, 2008 14:10
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Licenciatura em Matemática - UFSC
- Andamento: formado
 por lucas7 » Seg Fev 21, 2011 22:16
por lucas7 » Seg Fev 21, 2011 22:16
Ok! Entendido. Obrigado

O gênio, esse poder que deslumbra os olhos humanos, não é outra coisa senão a perseverança bem disfarçada.
Johann Goethe
-
lucas7
- Usuário Parceiro

-
- Mensagens: 53
- Registrado em: Ter Fev 15, 2011 19:43
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia de Controle e Automação
- Andamento: cursando
Voltar para Álgebra Elementar
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Divisão de fração algébrica 2
por lucas7 » Seg Fev 21, 2011 21:37
- 10 Respostas
- 5378 Exibições
- Última mensagem por lucas7

Ter Fev 22, 2011 17:26
Álgebra Elementar
-
- Fração Algébrica
por Lucio » Qua Dez 21, 2011 07:48
- 3 Respostas
- 2177 Exibições
- Última mensagem por fraol

Qua Dez 21, 2011 22:31
Polinômios
-
- Fração algébrica
por LuizCarlos » Sex Abr 20, 2012 13:09
- 5 Respostas
- 2318 Exibições
- Última mensagem por Cleyson007

Sex Abr 20, 2012 17:44
Álgebra Elementar
-
- Re: Fração algébrica
por LuizCarlos » Sáb Abr 21, 2012 09:10
- 5 Respostas
- 2596 Exibições
- Última mensagem por DanielFerreira

Sáb Abr 21, 2012 16:44
Álgebra Elementar
-
- Fração algébrica
por LuizCarlos » Sáb Abr 21, 2012 19:04
- 6 Respostas
- 2888 Exibições
- Última mensagem por Russman

Sáb Abr 21, 2012 20:40
Álgebra Elementar
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
Exercicios de polinomios
Autor:
shaft - Qua Jun 30, 2010 17:30

Então, o exercicio pede para encontrar

.
Bom, tentei resolver a questão acima desenvolvendo as duas partes em ( )...Logo dps cheguei em um resultado q nao soube o q fazer mais.
Se vcs puderem ajudar !
Assunto:
Exercicios de polinomios
Autor:
Douglasm - Qua Jun 30, 2010 17:53
Bom, se desenvolvermos isso, encontramos:

Para que os polinômios sejam iguais, seus respectivos coeficientes devem ser iguais (ax = bx ; ax² = bx², etc.):


Somando a primeira e a segunda equação:

Finalmente:

Até a próxima.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
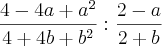 =
= 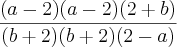 =
= 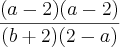 (meu desenvolvimento)
(meu desenvolvimento)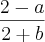
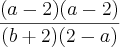 por -1, multiplicaria só o primeiro parênteses do numerado e do denominador, ficando:
por -1, multiplicaria só o primeiro parênteses do numerado e do denominador, ficando:  , corta o primeiro parentêses do numerador com o segundo parênteses do denominador, ficando
, corta o primeiro parentêses do numerador com o segundo parênteses do denominador, ficando  ou
ou 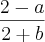 .
.

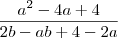

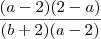





 .
.



