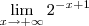
Usando propriedades de potência:

Como o denominador tende para o infinito e o numerador é constante, temos que essa fração tende a zero. Isto é:
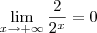
========

Dividindo o numerador e o denominador por

, nós temos que:

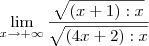
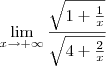


========

Temos um limite onde o numerador é constante e o denominador tende para 0, portanto a fração irá tender para o infinito. Como x aproxima-se de 5 pela esquerda (o que é representado pelo sinal de - após o 5), então x terá valores bem próximos de 5, porém menores do que 5. Logo, o denominador será negativo. Como o numerador é positivo, então o resultado será

.
========
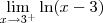
Já que x aproxima-se de 3, temos que o logaritmando se aproxima de 0. Quando o logaritmando aproxima-se de zero, sabemos que o valor do logaritmo neperiano tende a

.
Nesse caso, note que x aproxima-se de 3 pela direita (o que é representado pelo sinal de + após o 3), o que significa que x terá valores bem próximos de 3, porém maiores do que 3. Isso é relevante nesse caso, pois se colocássemos um valor próximo de 3 porém menor do que ele, então o logaritmando daria um número negativo, o que contraria a definição de logaritmo.
========
john escreveu:E gostaria também de perceber qual a diferença entre x->3+, x->3, e x->3-
A notação

significa que x tem valores próximos de a, porém maiores do que ele. Por exemplo, se

, então são possíveis valores de x: 3,01, 3,001, 3,0001, etc.
Por outro lado, a notação
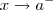
significa que x tem valores próximos de a, porém menores do que ele. Por exemplo, se
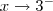
, então são possíveis valores de x: 2,99, 2,999, 2,9999, etc.
Por fim, a notação

significa que x tem valores próximos de a, tanto maiores ou menores do que ele. Por exemplo, se
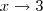
, então são possíveis valores de x: 2,99, 2,999, 2,9999, 3,01, 3,001, 3,0001, etc.
![\sqrt[]{x+1}/ \sqrt[]{4x+2} \sqrt[]{x+1}/ \sqrt[]{4x+2}](/latexrender/pictures/c87bd6ba8efa461b922b362c09b1d194.png)
![\sqrt[]{x}/ \sqrt[]{x^2-1} \sqrt[]{x}/ \sqrt[]{x^2-1}](/latexrender/pictures/9088f6731cf796841dbf70cd5902f53d.png)


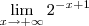

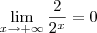

 , nós temos que:
, nós temos que:
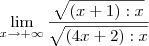
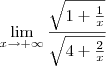



 .
.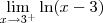
 significa que x tem valores próximos de a, porém maiores do que ele. Por exemplo, se
significa que x tem valores próximos de a, porém maiores do que ele. Por exemplo, se  , então são possíveis valores de x: 3,01, 3,001, 3,0001, etc.
, então são possíveis valores de x: 3,01, 3,001, 3,0001, etc.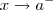 significa que x tem valores próximos de a, porém menores do que ele. Por exemplo, se
significa que x tem valores próximos de a, porém menores do que ele. Por exemplo, se 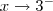 , então são possíveis valores de x: 2,99, 2,999, 2,9999, etc.
, então são possíveis valores de x: 2,99, 2,999, 2,9999, etc. significa que x tem valores próximos de a, tanto maiores ou menores do que ele. Por exemplo, se
significa que x tem valores próximos de a, tanto maiores ou menores do que ele. Por exemplo, se 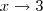 , então são possíveis valores de x: 2,99, 2,999, 2,9999, 3,01, 3,001, 3,0001, etc.
, então são possíveis valores de x: 2,99, 2,999, 2,9999, 3,01, 3,001, 3,0001, etc.
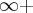 ? Já que tende para 3 pela direita, não deveria ficar
? Já que tende para 3 pela direita, não deveria ficar 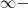 ?
?
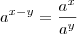

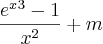 se x>0
se x>0 se
se 
![\exists c \in ]-3;\frac{-1}{2}[:f(c)=0 \exists c \in ]-3;\frac{-1}{2}[:f(c)=0](/latexrender/pictures/8bf033478b622326cf7a48ba21be9e67.png)
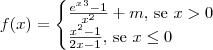
 , que é contínuo para x>0.
, que é contínuo para x>0.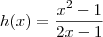 , que é contínuo para
, que é contínuo para 

 .
.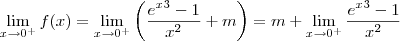

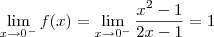
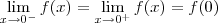
![\exists c \in\; ]-3;\frac{-1}{2}[ \; : f(c)=0 \exists c \in\; ]-3;\frac{-1}{2}[ \; : f(c)=0](/latexrender/pictures/d1e01a83fd4693a43d88f0250b054d19.png)
 . Você pode parar aqui. O máximo que você poderia fazer a partir daqui seria usar a aproximação
. Você pode parar aqui. O máximo que você poderia fazer a partir daqui seria usar a aproximação  para calcular um valor aproximado para f(10).
para calcular um valor aproximado para f(10).
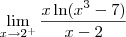
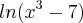 +x*
+x*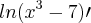



![[x\ln(x^3-7)]^\prime = x^\prime \ln(x^3-7) + x [\ln(x^3-7)]^\prime [x\ln(x^3-7)]^\prime = x^\prime \ln(x^3-7) + x [\ln(x^3-7)]^\prime](/latexrender/pictures/6048a1bbf09216d5c5c520ab72b74b23.png)
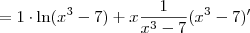

![[x\ln(x^3-7)]^\prime = \ln(x^3-7) + \frac{3x^3}{x^3-7} [x\ln(x^3-7)]^\prime = \ln(x^3-7) + \frac{3x^3}{x^3-7}](/latexrender/pictures/c9d44126110371f915b371b4f086a42c.png)
 a expressão
a expressão 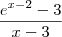 não tem qualquer restrição! Teríamos problema se x>2, pois aí o 3 estaria incluído o que faria aparecer um 0 no denominador.
não tem qualquer restrição! Teríamos problema se x>2, pois aí o 3 estaria incluído o que faria aparecer um 0 no denominador.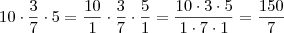 .
.