Como eu posso fatorar: x³-3x²+3x-1 e x^5-1
To com dificuldade com potências maiores que 2. Eu até consegui umas com 3, mas essa daí não está dando certo.
Obg.



runksoneck escreveu:Como eu posso fatorar:e
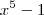
 . A forma fatorada desse polinômio será
. A forma fatorada desse polinômio será 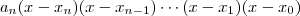 , onde
, onde  é cada uma das n raízes.
é cada uma das n raízes. , você precisa descobrir as 3 raízes da equação
, você precisa descobrir as 3 raízes da equação 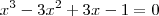 . Nesse caso, é fácil notar que 1 é uma raiz. Basta substituir x por 1 nessa equação e você verá que ela é válida. Como 1 é uma raíz, você pode reduzir o grau desse polinômio para achar as outras duas raízes. Para isso, você pode dividir o polinômio por (x-1). Nesse caso você irá encontrar
. Nesse caso, é fácil notar que 1 é uma raiz. Basta substituir x por 1 nessa equação e você verá que ela é válida. Como 1 é uma raíz, você pode reduzir o grau desse polinômio para achar as outras duas raízes. Para isso, você pode dividir o polinômio por (x-1). Nesse caso você irá encontrar 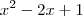 . Portanto, agora você tem que encontrar as raízes de
. Portanto, agora você tem que encontrar as raízes de  . Facilmente você irá encontrar que as duas raízes dessa equação são x'=x''=1. Portanto, teremos que:
. Facilmente você irá encontrar que as duas raízes dessa equação são x'=x''=1. Portanto, teremos que: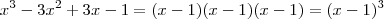
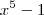 , você apenas precisa conhecer o produto notável
, você apenas precisa conhecer o produto notável  :
: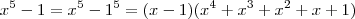



Usuários navegando neste fórum: Nenhum usuário registrado e 0 visitantes
![\frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}} \frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}}](/latexrender/pictures/981987c7bcdf9f8f498ca4605785636a.png)
![\sqrt[]{2} \sqrt[]{2}](/latexrender/pictures/f21662d1cabab6e8b273a4b6f1cd663a.png) (dica : igualar a expressão a
(dica : igualar a expressão a  e elevar ao quadrado os dois lados)
e elevar ao quadrado os dois lados)